trapez MATA: W trapezie ABCD dwusieczna kąta BAD jest prostopadła do ramienia BC w punkcie E. Wiedząc,że punkt E dzieli ramię BC w stosunku m : n licząc od wierzchołka B i m>n W jakim stosunku dwusieczna dzieli pole tego trapezu

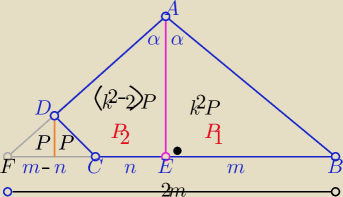
a@b: Z podobieństwa trójkątów ABF i DCF z cechy (kkk)

	2m		4m2
w skali k =		to k2=
	m−n		(m−n)2

P2		2
	= 1−		=..........
P1		k2

P2		m2+2mn−n2
	=
P1		2m2

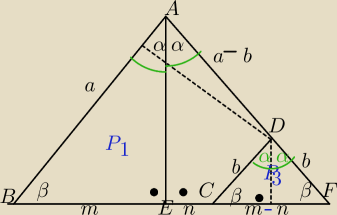a7: ABF − trójkąt równoramienny o ramieniu a CDF − trójkąt równoramienny o ramieniu b podobny do trójkąta ABF

	1
PABF=1/2a2sin2α=2P1 czyli P1=		a2sin2α
	4

P₁=P_ABE P₂=P_AEF P₃=P_CDF P₁=P₂ P₃=1/2b²sin2α

	(m−n)/2		m−n
sinα=m/a czyli a=m/sinα sinα=		czyli b=
	b		2sinα

P1		1/4a2sin2α
	=		=
P1−P3		1/4a2sin2α−1/2b2sin2α

	a2		m2/sin2α
=		=		=
	a2−2b2		m2sin2α−2(m−n)2/4sin2α

	2m2		2m2
=		=
	2m2−(m2−2mn+n2)		m2+2mn−n2

a@b:

a7:

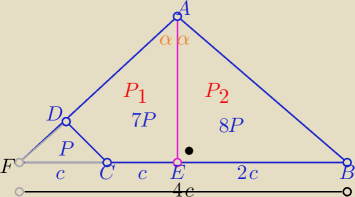a@b: Analogicznie dla podziału 2:1

P1		7		P2		8
	=		lub		=
P2		8		P1		7