Całka podwójna
Damian#UDM: Oblicz ∫∫
D√R2−x2−y2dxdy , gdzie D={(x,y): x
2+y
2−Rx≤0, y≤0}. Wykonaj rysunek.
Współrzędne biegunowe
| ⎧ | x=r*cos(α) | |
| ⎨ | y=r*sin(α) |
|
| ⎩ | J|α,r|=r | |
I w sumie tutaj mam największy problem, ponieważ nie wiem co to jest to R, zakładam, że po
prostu jakaś stała, a nie promień tego okręgu

0≤r≤Rcos(α)
π≤α≤2π
∫∫
D√R2−x2−y2dxdy=∫
2ππ∫
Rcos(α)0r
√R2−r2drdα
Podstawienie
R
2−r
2=t |'
−2rdr=dt
t
1≤r≤t
2
t
1=R
2−0
2=R
2
t
2=R
2−R
2cos
2(α)
∫
2ππ∫
Rcos(α)0r
√R2−r2drdα=
Dobra, znalazłem błąd

3 sty 10:18
Damian#UDM: Po podstawieniu i obliczeniu jednej całki otrzymałem:
3 sty 10:19
3 sty 13:48
Damian#UDM: To też mam

3 sty 14:51
chichi:
W takim razie nie rozumiem tych pytań...
"I w sumie tutaj mam największy problem, ponieważ nie wiem co to jest to R, zakładam, że po
prostu jakaś stała, a nie promień tego okręgu"
Jakiego okręgu? Stała, a nie promień, o co chodzi?

3 sty 15:02
Damian#UDM: Ważne, ze ja rozumiem 😁
3 sty 15:41
jc: Zamiana y na −y nic nie zmieni.
Można więc wybrać 0 ≤ a ≤ π/2.
| | R3 | | R3 | | 2R3 | |
Wynik = |
| ∫0π/2 (sin a)3 da = |
| ∫01 (1−c2) dc = |
| |
| | 3 | | 3 | | 9 | |
3 sty 21:03
Damian#UDM: Czemu taka parametryzacja kąta?
0≤α≤π2
4 sty 01:31
Damian#UDM: Ja nie zamieniałem y na −y tylko po podstawieniu otrzymałem minus

R
2−r
2=t |'
−2rdr=dt
dr=
dt−2r
4 sty 01:33
jc: Matematyka jest wystarczająca trudna i lepiej nie komplikować rachunków liczbami ujemnymi.
4 sty 13:35
Damian#UDM: A czemu występuje taka parametryzacja dla kąta alfa?
4 sty 17:52
jc: Oj, możesz wziąć kąty od −π/2 do 0 (bez zamiany y na −y)
4 sty 19:24
Damian#UDM: Tylko to jest zasięg dla 90 stopni, a u mnie jest 180 stopni i tego nie rozumiem. Mamy
ograniczenie y≤0, czyli wszystko pod osią x i znajdujące się w tym okręgu.
A pod osią x mam zasięg kąta od 180 stopni do 360 stopni. Co robię źle? Proszę o pomoc

11 sty 17:47
jc:
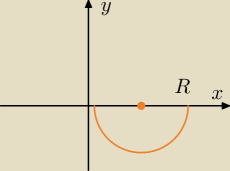
11 sty 23:46
jc: Półkole leży w prawej dolnej ćwiartce.
11 sty 23:49
 0≤r≤Rcos(α)
π≤α≤2π
∫∫D√R2−x2−y2dxdy=∫2ππ∫Rcos(α)0r√R2−r2drdα
Podstawienie
R2−r2=t |'
−2rdr=dt
0≤r≤Rcos(α)
π≤α≤2π
∫∫D√R2−x2−y2dxdy=∫2ππ∫Rcos(α)0r√R2−r2drdα
Podstawienie
R2−r2=t |'
−2rdr=dt



 R2−r2=t |'
−2rdr=dt
dr=dt−2r
R2−r2=t |'
−2rdr=dt
dr=dt−2r

