trójkąt
Rysiek:
Punkt M jest środkiem wysokości CD trójkąta równoramiennego ABC
o ramionach AC=BC
Punkt N jest rzutem prostokątnym punktuD na prostą BM
Wykaż,że trójkąt ACN jest prostokątny
2 sty 19:09
chichi:
Zrobiłeś Ty chociaż rysunek?
2 sty 20:36
Klara:
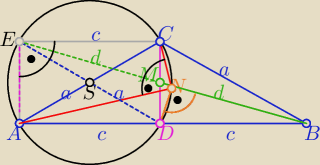
.................. a odpowiednie komentarze dopisz sam
teza: ΔCAN jest prostokątny
2 sty 21:10
Mila:
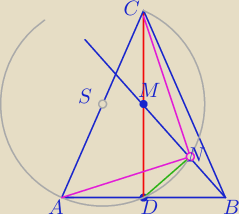
1) ΔABC−Δrównoramienny
2) M− środek wysokości CD, prosta BM
3) środek przeciwprostokątnej ΔADC
4) N − punkt przecięcia z prostą BM
5) ∡ANC− kat wpisany w okrąg oparty na średnicy
Wniosek?
2 sty 22:25
wredulus_pospolitus:
@Miluś ... na dobrą sprawę nigdzie nie wykazałaś skąd wiemy o (5)
2 sty 22:31
a7: wiemy bo ADC jest kątem prostym
2 sty 22:50
a7: (?)
2 sty 22:51
Mila:
A7, opisałam konstrukcję. Nie widziałam wpisu Ety , ciągle zaczynam , odchodzę
a potem już ktoś wpisuje rozwiązanie.
Trzeba jeszcze uzupełnić ,
że podane N jest rzutem prostokątnym punktu D na prostą BM.
2 sty 23:22
a7: no tak @Milu, ale skąd wiemy, że SA=SD=SC jest również równe SN? bo ja wpisu Ety nie
rozumiem akurat
(ja czasem zaczynam i klikam prawym przyciskiem na ">forum zadankowe> otwórz link w nowej
karcie" i sprawdzam czy już ktoś coś napisał)
2 sty 23:44
Mila:
Środkowa w Δprostokątnym poprowadzona z wierzchołka kata prostego
jest równa promieniowi okręgu opisanego na tym Δ.
3 sty 00:04
a7: a no i wszystko już jasne dzięki
3 sty 00:06
Mila:
Ja często zaczynam, zostawiam i wracam do rozpoczętego wpisu. Będę
teraz bardziej uważać i sprawdzać w innym okienku.
3 sty 00:06
a7: ale im więcej (sensownych) wpisów tym lepiej
3 sty 00:07
Mila:
Jeżeli poprowadzimy ( na moim rysunku ) średnicę NS , oznaczę punkt przecięcia K,
to ΔKND będzie prostokątny. Zatem N wcześniej wyznaczony jest szukanym rzutem ...
3 sty 00:11
a7: ale my mieliśmy "dany rzut"
3 sty 00:38