31 gru 11:38
a7: a inne odległości w ogóle nie są dane?
31 gru 11:57
a7: a próbowałeś w geogebrze?
31 gru 11:59
ite: pewnie KHAB jest półokręgiem, a KH jest średnicą
31 gru 12:00
a7: HK to średnica?
31 gru 12:00
ite: Jak to często bywa brakuje treści do zadania i można rozwijać domyślność.
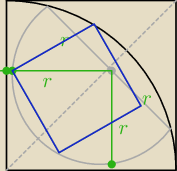
W tę ćwiartkę koła QOF można wpisać tylko jeden półokrąg, który byłby styczny w taki właśnie
sposób do QO i FO.
Więc można się domyślać, że to półokrąg a KH jest jego średnicą.
31 gru 12:07
a7:
31 gru 12:11
Feliks: Tak HK to średnica
31 gru 12:13
Feliks: A da się policzyć jakoś ten bok kwadratu?
31 gru 12:16
a7: myślimy
31 gru 12:18
a7: przynajmniej ja
31 gru 12:18
a7: z tego, co powiedziała ite wynika, że jest ten bok jednoznacznie określony chyba, więc
raczej da się go wyznaczyć
31 gru 12:26
a7: r=4√3
31 gru 12:34
a7: teraz trzeba jeszcze policzyć a
31 gru 12:35
a7: pomyłka r=2√3
31 gru 12:37
31 gru 12:41
Feliks: Mam pytanie a moze r=a

31 gru 12:54
a7: nie wiem, trzebaby to jakoś wydedukować
31 gru 13:09
Mila:
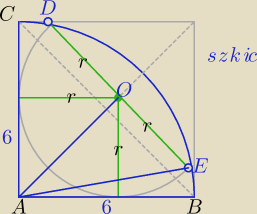
1) Promień półkola
|AO|=r
√2
|AE|=6
W ΔAEO:
6
2=r
2+(r
√2)
2
36=3r
2
r
2=12
r=2
√3
31 gru 18:09
Feliks: Ok a czy bok kwadratu to r?
31 gru 18:10
Mila:
Raczej nie, teraz muszę iść do zajęć domowych.
Spojrzę później, ale to
A7 pewnie napisze

Sylwestrowo pozdrawiam

31 gru 18:22
a7: ja nie wiem. Pozdrawiam już prawie Noworocznie

31 gru 18:30
chichi:
@
Feliks natomiast ja z @
Mila się nie zgodzę i powiem, że długość boku kwadratu jest
równa długości 'r' i to szukane pole to właśnie 12 [cm
2], szczęśliwego nowego roku

31 gru 21:18
Mila:
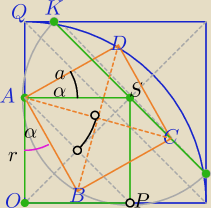
Wydaje mi się , że jednak a=r.
Kwadrat ABCD jest obrazem kwadratu AOPS w obrocie o kąt α wokół punktu A.
Nie widzę na razie , jak to wykazać. Z konstrukcji ( szkicu) taki mój wniosek.
31 gru 21:23
Mila:
Też się zgadzam z moim zapisem 18:22
31 gru 21:24
Mila:
Ubiegłeś mnie
chichi, smażyłam rybkę i dopiero teraz jestem na forum

31 gru 21:25
Feliks: i jak ktoś ma pomysł?
2 sty 11:43
a7: a masz treść zadania to może by się udało znaleźć w necie gdzieś? chociaż chichi chyba wie
ale na razie się nie odzywa
2 sty 13:50
a7: ok mam pomysł, ale nie wiem czy dobry
2 sty 13:51
chichi:
Ale co tutaj nadal jest niejasne, bo nie rozumiem?

2 sty 14:02
a7: skąd wiadomo, że r=a
2 sty 14:06
Feliks: No tak chodzi o to wykazanie a=r
2 sty 14:10
chichi:
A no tak.. To trzeba co nieco zauważyć (korzystam z rysunku i oznaczeń @
Mila):
(1) |∡CBA| = 270
o (mowa o kącie zewnętrznym!)
| | 1 | |
(2) |∡OSA| = 45o ⇒ |∡CSA| = 90o+45o = 135o = |
| |∡CBA| |
| | 2 | |
(3) |BC| = |BA|
No to wniosek jest prosty: B to środek okregu, zatem |BC| = |BA| = |BS| = r
Nie było to aż takie oczywiste, ale też nie trudne

2 sty 15:01
a7: fajne

2 sty 15:32


 1) Promień półkola
|AO|=r√2
|AE|=6
W ΔAEO:
62=r2+(r√2)2
36=3r2
r2=12
r=2√3
1) Promień półkola
|AO|=r√2
|AE|=6
W ΔAEO:
62=r2+(r√2)2
36=3r2
r2=12
r=2√3
 Sylwestrowo pozdrawiam
Sylwestrowo pozdrawiam


 Wydaje mi się , że jednak a=r.
Kwadrat ABCD jest obrazem kwadratu AOPS w obrocie o kąt α wokół punktu A.
Nie widzę na razie , jak to wykazać. Z konstrukcji ( szkicu) taki mój wniosek.
Wydaje mi się , że jednak a=r.
Kwadrat ABCD jest obrazem kwadratu AOPS w obrocie o kąt α wokół punktu A.
Nie widzę na razie , jak to wykazać. Z konstrukcji ( szkicu) taki mój wniosek.



