Układ równań

Układ równań Algorytm: Obliczając jedno zadanie otrzymałem pewny układ równań z 2 niewiadomymi:

⎧	y² = 4+x² − 2x
⎩	(2√7 − y)² = 16+x²−4x

Wszystko, co wiem próbowałem i mi nie wychodzi, jak można to obliczyć? xD

30 gru 23:49

Algorytm: Otrzymywałem albo takie równanie −28 + 4√7y = −12 + 2x Albo otrzymywałem równanie: 0 = 27y² + 28√7y + 52, otrzymując z delty −128

30 gru 23:53

a7: a możesz dać oryginalną treść zadania?

30 gru 23:54

a7: https://www.wolframalpha.com/input/?i=y%5E2+%3D+4%2Bx%5E2+%E2%88%92+2x++%26+%282%E2%88%9A7+%E2%88%92+y%29%5E2+%3D+16%2Bx%5E2%E2%88%924x%09

30 gru 23:58

a7: x=4/3 y=2√7/3

30 gru 23:59

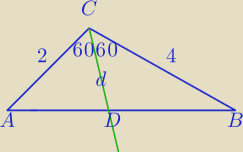
Algorytm: W trójkącie ABC dane sa: |BC| = 4cm, |AC| = 2cm, |<ACB| = 120. Wyznacz długość odcinka dwusiecznej kąta ACB, zawartego w tym trójkącie. No i oznaczyłem sobie, że: x = |CD|; y = |AD|; b = |AB| Póżniej zrobiłem układ równań, gdzie:

⎧	y² = 4 + x² − 2 * 2 * x * cos60
⎩	(b−y)² = 16+x² − 2 * x * 4 * cos60

30 gru 23:59

Mila: Wykonaj potęgowanie w drugim równaniu i odejmij stronami równania. Następnie wyznacz x i wstaw do pierwszego równania. Liczę.

30 gru 23:59

Algorytm: Ale w jakim sensie potęgowanie w drugim równaniu? xd

31 gru 00:01

Mila:

	1		√3
P_Δ=		24sin120⁰=4
	2		2

P_Δ=2√3

	1		1
2√3=		2d sin60⁰ +		d4*sin60^o
	2		2

	√3		√3
2√3=d*		+2d*
	2		2

	1
2=		d+d
	2

3
	d=2
2

	2
d=2*
	3

	4
d=
	3

======

31 gru 00:08

a7: b=2√7 z tw. o dwusiecznej y/2=(2√7−y)/4 czyli y=2√7/3 teraz wstawiamy do pierwszego imamy x=4/3

31 gru 00:08

Algorytm: Wow, dzięki, nigdy do tego nie domyśliłbym się xd

31 gru 00:19

Mila: 1) (2√7−y)²=x²−4x+16 28−4√7y+y²=x²−4x+16 y²=x²−4x+4√7y−12 y²=x²−2x+4 ============ (−) 2) 0=−2x+4√7y−16 2x=4√7y−16 x=2√7y−8 3) (2√7y−8)²−4√7y+16+4 y²=28y²−32√7y+64−4√7y+20 27y²−36√7y+84=0 /:3 9y²−12√7y+28=0 Δ=144*7−4*9*28=0

	12√7
y=
	18

	2√7
y=
	3

	4
x=
	3

=====

31 gru 00:22

Mila: Dobranoc emotka

31 gru 00:25

a7: Dobrej nocy!

31 gru 00:29

Algorytm: Dobranoc i dziękuje emotka

Tylko mam pytanie do jednej części z rozwiązania. Mając: y² = x² − 4x + 4√7y − 12 A w następnej linii mamy: y² = x² −2x + 4, dlaczego? Co się stało z 4√7y − 12?

31 gru 00:59

a7: to jest drugie równanie

31 gru 01:01

a7: potem odejmujemy stronami (−)

31 gru 01:01

a7: "to jest drugie równanie" − czyli twoje pierwsze

31 gru 01:06

Algorytm: Aha, no tak, dziękuję xd

1 sty 22:36