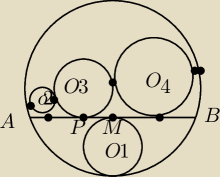
AB jest cięciwą okręgu o promieniu r, punkt M jest środkiem AB. Okrąg O1 o promieniu r1 jest
styczny wewnętrznie do danego okręgu oraz do AB w punkcie M. Niech punkt P∊AB, P≠A,B,M. Okrąg
O3 ma taki sam promień jak okrąg O1 i jest styczny do AB w P. Okręgi O2 i O4 o promieniach
r2 i r3 są styczne do AB i do okręgu O3 (rys) oraz okręgu o cięciwie AB. Wykaż ze
r=r1+r2+r3.
