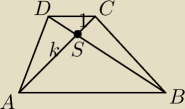
W nierównoramiennym trapezie klaudia2137: W nierównoramiennym trapezie ABCD (AB || CD) przekątne AC i BD przecinają się w punkcie S takim, że AS:SC=k:1. Oblicz stosunek pola trójkąta CDS do pola trapezu ABCD. Jak to zrobić? 3 klasa liceum p. roz.

ite: 1/ ΔCDS i ΔABS są podobne (dlaczego?) w skali k:1. Stąd można wyznaczyć stosunek ich pól. 2/ ΔCDS i ΔADS mają wspólną wysokość a stosunek podstaw wynosi k:1. Też można wyznaczyć stosunek ich pól. Tak samo jest z ΔCDS i ΔBSC.

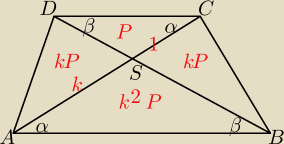Artur: P − pole trójkąta CDS

Bona: P(trapezu)= (k+1)²*P

	P		1
		=
	P(trapezu)		(k+1)2

Pozdrawiam Króla Artura

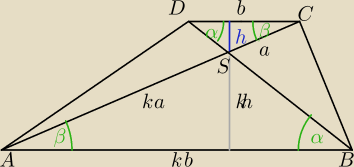a7: trójkąty DCS i ABS są do siebie podobne (k,k,k − ∡ASB=∡DSC − kąty wierzchołkowe, ∡CDS=∡ ABD oraz ∡ACD=∡CAB− kąty naprzemianległe) czyli ich boki i wysokości są podobne w skali k SC oznaczam a SA będzie równe ka DC=b AB=kb wyoskość DCS=h wysokośćASB=kh

	1
PDCS=		bh
	2

PDCS		1   bh 2		bh
	=		=		=
PABCD		(kb+b)   *(kh+h) 2		2b(k+1)   *h(k+1) 2

	bh		1
=		=
	bh(k+1)2		(k+1)2