29 gru 18:25
anonim123: czym się różni jedna strona inkluzji od drugiej?
29 gru 18:37
ite:
Wytrwale nie podajesz treści zadań, więc trzeba zgadywać.
Czy zapis f(A) może oznaczać obraz zbioru A w funkcji f ?
29 gru 21:33
29 gru 21:40
ite:
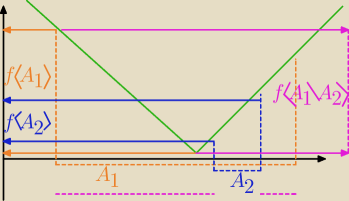
Czy daje się z tego rysunku odczytać zbiory:
f(A1\A2)
f(A1)\
f(A2)
Jeśli tak, to jest to kontrprzykład dla równości z pkt e/.
29 gru 21:54
ite: I widać to, o co pytasz: różnicę między zbiorami po obu stronach inkluzji czyli między f(A1\A2)
i f(A1)\f(A2).
29 gru 21:56
anonim123: ja tego tutaj nie widzę możesz jakoś opisać rysunek?
29 gru 22:17
anonim123: Może odpisać ktoś inny również
30 gru 11:09
ite:
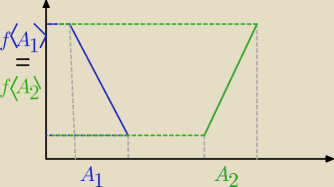
Narysuję trochę inny kontrprzykład do pktu e/, będzie lepiej widać zależności:
wybieram zbiory rozłączne i dobieram f, żeby spełnione były warunki
A
1 ∩ A
2=∅ oraz f(A
1) = f(A
2) ≠ ∅.
Wtedy A
1\A
2=A
1 stąd f(A
1\A
2) = f(A
1) czyli obrazem różnicy jest (niepusty) obraz
pierwszego zbioru.
a jednocześnie f(A
1) \ f(A
2) =∅, obrazy obu wybranych zbiorowa są jednakowe, więc ich ich
różnica jest zbiorem pustym.
Czyli obraz różnicy f(A1\A2) oraz różnica obrazów f(A1)\f(A2), to dwa różne zbiory..
30 gru 11:17
ite:
11:09 ← może ktoś inny potrafi wytłumaczyć jaśniej, jeśli mnie się nie udało.
30 gru 11:18
