Konstrukcja dziesięciokąta wykorzystująca proporcje proste
Mariusz:
https://imgur.com/a/oQ5LjHw
Jak skonstruować dziesięciokąt zgodnie z tym co na rysunku
29 gru 04:27
a7: 1. mamy dany okrąg a w nim pięciokąt foremny
2. rysujemy środkową kąta AOB
3. rysujemy A'B' (na odpowiednio odległym punkcie środkowej kata AOB wyznaczamy punkt przez
który prowadzimy symetralną i rysujemy odcinek A'B')
4.rysujemy proste A'A i B"B przechodzące odpowiednio przez półproste OA i OB i mamy R.
29 gru 16:51
a7: poprawka: 4. rysujemy proste A'A i B'B ....
29 gru 16:53
Mariusz:
A jakiś dokładniejszy opis tej konstrukcji bo utknąłem
na tej konstrukcji tego odcinka A'B'
Wg mnie problem z twoim opisem konstrukcji jest tutaj
"na odpowiednio odległym punkcie środkowej kata AOB wyznaczamy punkt przez
który prowadzimy symetralną i rysujemy odcinek A'B' "
Ten krok nie jest sprecyzowany
Mamy z góry zadaną długość tego odcinka AB i chyba tak dowolnie nie możemy
wybrać tego środka odcinka A'B'
Na razie skonstruowałem środkową kąta AOB
oraz te proste zaznaczone na czarno
31 gru 00:40
a7: chodziło mi o to, żeby ten odcinek A'B' był dalej (od środka okręgu) niż odcinek AB
31 gru 00:45
a7:
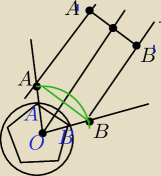
31 gru 00:50
a7: oj pomyliłam się w rysunku
31 gru 00:51
a7:
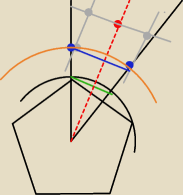
31 gru 00:55
a7: czy już wiesz o co mi chodzilo?
31 gru 01:00
a7: ten środek odcinka A'B' po prostu wg rysunku musi być gdzieś dalej − musi się zmieścić na
kartce
31 gru 01:03
a7: A'B' musi być "węższe" niż ramiona kąta AOB
31 gru 01:05
a7: A'B' musi być na tyle daleko aby mieściło się między ramionami kata AOB.
31 gru 01:08
a7: 1. rysujemy dwusieczną kąta AOB (czerwona przerywana na moim rysunku)
2. wyznaczamy punkt na tej dwusiecznej (w dowolnym miejscu ale lepiej zostawić trochę miejsca
to wyjdzie jak na rysunku wzorcowym)
3. przez wyznaczony punkt kreślimy symetralną tej dwusiecznej
4. na tej symetralnej kreślimy odcinek A'B' tak aby jego środek był w tym wybranym wcześniej
punkcie
5.przez punkty A' i B' prowadzimy dwie proste prostopadłe do tej symetralnej
6. proste prostopadłe z punktu 5 przetną ramiona kąta AOB w punktach A oraz B
wyznaczając bok dziesięciokąta
7. szukany promień R to odcinek łączący środek pierwotnie danego okręgu z wyznaczonymi w
punkcie 6 punktami.
31 gru 02:24
Mariusz:
Autor tego rysunku napisał że proste tego samego koloru są równoległe
i tutaj chyba prosta O'A' miała być niebieska
Długość odcinka A'B' jest z góry zadana
Nie dałoby tu rady skorzystać z twierdzenia Talesa bądź podobieństwa figur
Duża liczba prostych równoległych wskazywałaby na możliwość użycia
twierdzenia Talesa bądź podobieństwa figur
Jeżeli wybierzemy środek odcinka A'B' w miarę dowolnie to po poprowadzeniu
równoległej do AB (gdzie A oraz B to punkty na okręgu k)
i przechodzącej przez punkt ten wybrany środek możemy nie otrzymać
odcinka o takiej długości jaką byśmy chcieli
Konstruowane figury mają być podobne
(równość miar kątów ma być zachowana a długości boków mają być proporcjonalne)
To też autor tego rysunku zdążył napisać
Niestety autor rysunku już nic więcej nie napisze
31 gru 02:32
a7: nie no, ja nie rozumiem czego Ty nie rozumiesz, mi się wszystko wydaje zrozumiałe
czy dobrze rozumiem, że jest dany okrąg z pięciokątem oraz odcinek AB jako długość boku
docelowego dziesięciokąta?
31 gru 02:40
a7: i chcesz to wyznaczyć konstrukcyjnie
31 gru 02:40
a7: tu nie chodzi o policzenie tylko o wyznaczenie konstrukcyjne, więc o co Ci chodzi z tym tw.
Talesa
31 gru 02:42
a7: AB to u mnie niebieski odcinek na rysunku 00:55
31 gru 02:43
Mariusz:
Ja kostruowałem tak jak on sugerował
czyli konstruując proste równoległe, środkową AOB ,
a prostą O'A' z odłożenia kąta choć na moje oko też można z prostej równoległej
31 gru 02:44
a7:
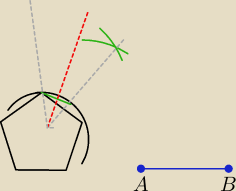
ale jak zaczynamy rysować to mamy tylko okrąg z pieciokatem z katem AOB oraz z odcinkiem
AB wolnym
31 gru 02:47
a7: środkowa AOB czyli dwusieczna kąta AOB
31 gru 02:48
a7: no to wszystko się zgadza
31 gru 02:48
Mariusz:
Tak ale z twierdzenia Talesa bądź podobieństwa figur układasz proporcje które
możesz później wykorzystać
31 gru 02:49
a7: nie rozumiem czego nie rozumiesz...
31 gru 02:50
a7: ale tu chodzi o konstrukcję geometryczną, a nie o obliczenie, czy o jedno i drugie?
31 gru 02:51
a7: pytałeś na poczatku jak skonstruować dzieisęciokat zgodnie z tym co na rysunku, no i to jest
dla mnie zrozumiałe nie rozumiemczego nie rozumiesz i dlaczego chcesz tutaj "wciskać"tw.
Talesa
31 gru 02:52
a7: czerwone proste z rysunku wyjściowego sa równoległe zgadza się
31 gru 02:53
a7: u mnie (00:55) zielona, niebieska i szara
31 gru 02:54
a7: środek odcinka AB wyznaczamy geometrycznie ale na dwusiecznej wybieramy dowolnie jego
umiejscowienie, potem jej symetralną i nanosimy po połowie odcinka A'B' może o to Ci chodzi?
31 gru 02:56
Mariusz:
Jeżeli chodzi o twierdzenie Talesa to pytanie pomocnicze
Jak skonstruujesz odcinek będący iloczynem i jak uzasadnisz poprawność konstrukcji ?
Tu mamy do czynienia z proporcjonalnością odcinków czyli w pewnym sensie mnożenie jest
Długość odcinka AB jest z góry zadana i tego środka nie można tak dowolnie wybrać
31 gru 03:02
a7:
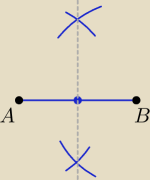
środek odcinka
AB wyznaczamy na zadanym odcinku potem go nanosimy połowami na symetralną
dwusiecznej AOB
(autor rysunku ma na rysunku punkty A oraz B dlatego ja te oznaczające bok dziesięciokąta
pogrubiam {P[A]] oraz {P[B]]
31 gru 03:06
a7: sorry, ale chyba komplikujesz coś czego autor rysunku nie miał na myśli
31 gru 03:07
a7: tu wszystko prostymi ruchami można zrobić
31 gru 03:07
a7: 03:06 miało być "A oraz B"
31 gru 03:08
a7: 03:06 nie na symetralną tylko na prostą prostopadłą do dwusiecznej (przepraszam za nieścisłość)
31 gru 03:16
a7: na czerwony punkt z rysunku 00:55 nanosimy połowy (zadanego) odcinka AB i mamy punkty A'
oraz B'
teraz przez te punkty prowadzimy proste prostopadłe do szarej prostej (A'B') i na
przecięciu z ramionami kata AOB otrzymujemy punkty A oraz B
czyli mamy już zadany bok dziesięciokąta w tej konstrukcji geometrycznej (o co nam chodziło)
oraz promień okręgu, w który ten dziesięciokąt jest wpisany
31 gru 03:29
a7: a to do pracy licencjackiej?
31 gru 03:30
a7: zaliczeniowej?
31 gru 03:30
31 gru 04:34
Mariusz:
"czy dobrze rozumiem, że jest dany okrąg z pięciokątem oraz odcinek AB jako długość boku
docelowego dziesięciokąta?"
Tak z grubsza tak Jeżeli odcinek AB nie jest położony na płaszczyźnie we właściwym miejscu
to z tego można by wyjść
(na początku konstrukcji
znamy długość odcinka AB ale nie wiemy gdzie on się na płaszczyźnie znajduje)
Tutaj tak naprawdę chodzi mi o sposób konstrukcji wykorzystujący tzw proporcje proste
a ten dziesięciokąt to tylko przykład
bo jeśli chodzi o konstruowanie wielokątów o danej długości boku
to całkiem niedawno wyprowadziłem dwa dość ogólne sposoby konstrukcji
"a to do pracy licencjackiej?
zaliczeniowej?"
Nie musisz ironizować
Zmodyfikowałaś ten jego rysunek
U niego konstruowane trójkąty są podobne (cecha kąt kąt kąt)
a u ciebie jak to jest ?
Tutaj znam miarę kąta i tak na dobrą sprawę położenie
tego odcinka A'B' mógłbym policzyć z trygonometrii ale chciałem bez tego
Po znalezieniu punktów A
Jeżeli chodzi o konstruowanie wielokątów foremnych to samemu po prawie 30 latach
jak to miałem w szkole wyprowadziłem dwie dość ogólne konstrukcje
które działają o ile potrafimy skonstruować potrzebne kąty
(Jedna konstrukcja bazuje na konstrukcji trójkąta równoramiennego
−tutaj potrzebnym kątem jest kąt środkowy
Druga konstrukcja bazuje na konstrukcji kąta zewnętrznego − przyległego do wewnętrznego)
Jedyne co miałem do dyspozycji to pomocnicze konstrukcje z tablic
Jak ty piszesz te pogrubione litery ?
Wklejasz z zewnętrznego edytora czy jak
31 gru 05:04
a7: pogrubione litery pisze się [ P [ litera ] ] bez spacji
31 gru 05:18
a7: nie ironizowałam
31 gru 05:19
a7: pytałam się z ciekawości
31 gru 05:19
a7: u mnie tez trójkaty są podobne
31 gru 05:20
a7: czy zauważyłeś, że punkt B na okręgu też trzeba wyznaczyć na początku konstrukcji?
31 gru 05:21
a7: bo ja dalej nie rozumiem czego Ty nie rozumiesz...
31 gru 05:21
a7: tutaj nie którzy się zgadują na discordzie jak mi podasz swojego (np.tymczasowego) maila to
odpisze i się możemy zgadać to będzie łatwiej (?), ale ja nie jestem jakąs specjalistką
31 gru 05:22
a7: położenie odcinka A'B' jest dowolne
31 gru 05:23
a7: byleby był prostopadły to dwusiecznej i przecinał tę dwusieczną w swojej połowie
31 gru 05:24
a7: ale Ty w takim razie nie jesteś tym tutejszym Mariuszem m.in. od całek? (skoro nie umiesz
pisać pogrubionych liter?0
31 gru 05:27
a7: poprawki: niektórzy, do dwusiecznej , pogrubionych liter)
31 gru 05:28
a7: (to znaczy ja nie mam discorda, ale jakoś się możemy zgadać)
31 gru 05:29
a7: z tego, co napisałeś 05:04 mam wrażenie, że masz zaćmienie umysłu jak się robi konstrukcje
geometryczne
druga możliwość to taka, że Twoim naukowym celem jest ta inna rzecz i ta (pomocnicza
konstrukcja) namieszała Ci w głowie a ja nie wiem do czego tak właściwie dążysz, jednak nadal
podtrzymuję , że moja konstrukcja (odczytanie intencji autora pierwotnego rysunku) wydaje mi
się prawidłowe
31 gru 05:39
a7: i nie jest to ironia tylko próbuję zrozumieć czego nie rozumiesz
31 gru 05:40
a7: mogę przesłać Ci link do tablicy wirtualnej i wytłumaczyć interaktywnie, to może się uda
31 gru 05:48
a7:
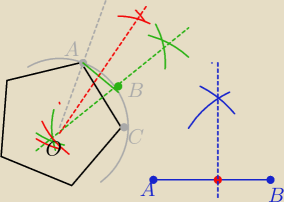
1. wyznaczamy punkt B
2. wyznaczamy dwusieczną (zwaną w pierwotnym rysunku środkową kata AOB)
3. dzielimy dany odcinek
AB na pół
31 gru 06:25
a7:
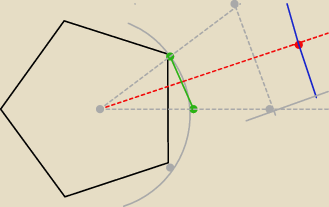
4. na dwusiecznej wybieramy (dowolonie punkt, do którego kreslimy prosta prostopadłą)
5. na tę prostą prostopadłą nanosimy połówki odcinka
AB
6. kreślimy proste prostopadłe do niebieskiej prostopadłej do dwusiecznej i one wyznaczają nam
punkty
A oraz
B
7. zrobione

31 gru 06:32
a7: czy teraz już wiadomo dlaczego taka kolejność o które trójkąty są do siebie podobne (jesli to w
ogóle ma tu znaczenie)
31 gru 06:33
a7: ?
31 gru 06:33
Mariusz:
"położenie odcinka A'B' jest dowolne"
a to na pewno będziemy mieli taki sam rysunek jak u niego
Autor tego rysunku zmarł jakiś miesiąc i trzy tygodnie temu
Jeśli chodzi o punkt B na okręgu k to on do jego znalezienia
poprowadził prostą równoległą
Jeżeli środek odcinka A'B' wybierzesz dowolnie to albo trójkąt A'O'B' nie zachowa
cechy (kąt kąt kąt) i nie będzie podobny do trójkąta AOB (gdzie A oraz B na okręgu k)
Nie napisał szczegółowego opisu konstrukcji ale chyba wiem jak skonstruować ten
trójkąt podobny A'O'B'
aczkolwiek rzeczywiście będzie dość sporo kroków konstrukcji
31 gru 06:38
a7: punkt B na okręgu k wyznaczamy (moim zdaniem) przez symetralną dla AC (czyli przez symetralną
boku pięciokąta aby mieć propocjonalny (ale nie w tym Twoim znaczeniu) wyjściowy bok
dziesięciokąta), a ta prosta jest albo pomocnicza albo ma inne znaczenie)
31 gru 06:43
a7: O' powstaje automatycznie przez przecięcie przez dwusieczną okręgu k, i trójkąt A'O'B' tez
powstaje "przy okazji"
31 gru 06:45
a7: położenie odcinka A'B' jest dowolne gdyż może być nawet między odcinkiem AB i odcinkiem AB
i też wyjdzie dziesięciokąt foremny, ale oczywiście jesli narysujesz ten czerwony punkt
odpowiednio dalej to będziesz miał podobnie jak na rysunku pierwotnym, chodzi (moim zdaniem) o
to, żeby skonstruować dziesięciokąt foremny o zadanym boku, zadaną metodą, anie gdzie ma być
który odcinek tylko aby była jasna metoda, która podążał autor
31 gru 06:48
a7: tzn. rozumiem, że autor wymyślił, ja próbowałam za nim podążyć...
31 gru 06:49
a7: Ś.p Autor zrobił notatki do rysunku, które pozwalają się domyslić tego, co ja Ci tu bardzo
szczegółowo rozpisałam, mam wrażenie, że może ja zbyt prosto podchodze do tematu, ale mi się
wszytsko zgadza, a Ty mam wrażenie że próbujesz skomplikować prostą sprawę
31 gru 06:53
Mariusz:
"((jesli to w ogóle ma tu znaczenie)"
Jak to podobieństwo trójkątów nie ma tutaj znaczenia przecież
mając skonstruowany pięciokąt , skonstruowaliśmy dwusieczną kąta środkowego
przez co dostaliśmy kąt środkowy dziesięciokąta
i teraz musimy zmienić proporcjonalnie długości boków
czyli dalsze konstrukcje muszą zachowywać podobieństwo
On napisał że po znalezieniu kąta środkowego wystarczy rysunek przeskalować
aby długość boku była równa zadanej długości
Zmodyfikowałaś nieco jego sposób co nie znaczy że nie jest poprawny
31 gru 06:56
a7: dlaczego musimy zmienić (proporcjonalnie) długości boków? zrozumiałam, że AB jest dany
31 gru 07:00
a7: i tak pisze AUTOR
31 gru 07:03
a7: (AUTOR rysunku)
31 gru 07:03
a7: a faktycznie, że chyba coś zmodyfikowałam
31 gru 07:14
a7: to mi się wydaje, że ta metoda jest jeszcze bardziej uniwersalna, bo już nie trzeba nic
przeskalowywać
31 gru 07:15
a7: czyli też szybsza oraz prostsza
31 gru 07:16
a7: z tymże ja chyba nie wiem jaki to ma związek z proporcjami, gdyż ja (tylko) wiem jak
skonstruować po prostu dziesięciokąt o zadanym boku mając dany okrąg z wpisanym pięciokątem ,
nie wiem gdzie tu proporcjonalność, także może dlatego ta modyfikacja jest zbytnim
uproszczeniem (?)
31 gru 07:20
Mariusz:
Gdybyśmy chcieli narysować konstrukcję identyczną jak konstrukcja ś. p. autora to
Na boku wyznaczamy odcinek o długości będącej skalą podobieństwa
(zgadnij z czego korzystamy)
Jeden z punktów A' bądź B' znajdujemy skalując jeden z boków
skonstruowanego wcześniej trójkąta
(zgadnij z czego korzystamy)
Odcinek A'B' znajdujemy prowadząc prostą równoległą do AB i
przechodzącą przez skonstruowany wcześniej punkt
Mając skonstruowane dwa boki trójkąta trzeci też dostaniemy
Gdy już będziemy mieli odcinek A'B' to odcinek AB też znajdziemy
(Tak jak ś. p. autor sugerował z prostych równoległych do środkowej AOB)
Twoja konstrukcja nie jest aż tak do końca zgodna z jego
konstrukcją ale za to jest mniej skomplikowana
31 gru 07:25
a7: ok, w każdym bądź razie rozumiem, że Twój problem już rozwiązany?
31 gru 07:28
Mariusz:
Jest dana tylko długość boku , nie wiemy na początku konstrukcji gdzie na płaszczyźnie
ten odcinek AB się znajduje
31 gru 07:29
Mariusz:
Chyba że znajdziesz prostszy sposób na uzyskanie tego samego efektu
Jeszcze sprawdzę w Geogebrze co wyjdzie z tej konstrukcji
31 gru 07:32
a7: no oczywiście, ale myślałam, że już dwa razy wytłmaczyłam jak to zrobić i nawet proponowałam
zgadanie się poza forum, także ja już się chyba wyłączam z wątku, może Mila lub Eta
lub jeszcze ktoś Ci wyjaśni
31 gru 07:33
a7: no przecież uzyskałam efekt dziesięciokąta z wyznaczeniem gdzie na płaszczyźnie znajdzie się
zadany odcinek AB względem okręgu
31 gru 07:34
a7: naprawde nie rozumiem czego nie rozumiesz , chyba masz na myśli jeszcze głebszą treść tego
zagadnienia albo wógle nie podążyłes za moim (jednak cierpliwym) i dwukrotnym tłumaczeniem
31 gru 07:35
a7: jeśli chodzi o wykorzystanie proporcji odcinków w tym rysunku to musiałabym się zastanowić, ale
zaraz spróbuję
31 gru 07:51
a7: nie chyba tego nie umiem tak łatwo zaadaptować do swojego sposobu patrzenia
31 gru 07:59
Mariusz:
Wypróbowałem ten jego sposób w Geogebrze przy czym trzymałem się ściśle jego konstrukcji
bez żadnych modyfikacji i działa ale było dużo kreślenia
Gdybyśmy mieli zrealizować ją na papierze to trzeba by było zaopatrzyć się także w
dobrze zaostrzony ołówek z gumką liniał i cyrkiel
No autor tego rysunku nazwał przedstawiony tutaj sposób konstrukcji metodą proporcji prostych
Ułóż sobie z tw Talesa proporcje które pomogą ci znaleźć odcinek o długości będącej
skalą podobieństwa a następnie przypomnij sobie jak się ilustrowało twierdzenie Talesa
Następnie ułóż sobie z tw Talesa proporcje które pozwolą ci przeskalować jeden z boków
a następnie przypomnij sobie jak się ilustrowało twierdzenie Talesa
Pozostałych boków nie trzeba skalować bo wystarczy poprowadzić prostą równoległą
aby znaleźć bok A'B'
Trzeci bok tego podobnego trójkąta dostajemy za darmo jednak nie jest on nam potrzebny
31 gru 09:07
Mariusz:
" naprawde nie rozumiem czego nie rozumiesz , chyba masz na myśli jeszcze głebszą treść tego
zagadnienia albo wógle nie podążyłes za moim (jednak cierpliwym) i dwukrotnym tłumaczeniem"
Ja po prostu chciałem dokładnie odtworzyć tę konstrukcję z jego rysunku
Jak się przyjrzeć to on narysował też dwa okręgi
a ja tych okręgów nie potrzebowałem
Jak ta twoja konstrukcja wygląda na animacji ?
31 gru 09:28
a7: ja nie robiłam animacji
31 gru 09:36
Mariusz:
Tak na dobrą sprawę to nie trzeba konstruować odcinka o długości równej skali podobieństwa
i aby przeskalować jeden z boków trójkąta AOB w celu otrzymania trójkąta A'O'B'
wystarczy raz zastosować twierdzenie Talesa
1 sty 17:02
Mariusz:
Trójkąt AOB można przeskalować bez konstruowania pomocniczego trójkąta A'O'B' więc
jeśli musimy korzystać z pomocniczego odcinka A'B' to twoja propozycja wydaje się być
rozsądna mimo iż nie dostaniemy dokładnie tego co na rysunku
2 sty 09:05
a7: no w każdym bądź razie otrzymamy dziesięciokąt o zadanym odcinku AB − chyba o to
chodziło....(?)
2 sty 09:13
Mariusz:
Jeszcze jedno
1. rysujemy dwusieczną kąta AOB (czerwona przerywana na moim rysunku)
2. wyznaczamy punkt na tej dwusiecznej (w dowolnym miejscu ale lepiej zostawić trochę miejsca
to wyjdzie jak na rysunku wzorcowym)
3. przez wyznaczony punkt kreślimy symetralną tej dwusiecznej
4. na tej symetralnej kreślimy odcinek A'B' tak aby jego środek był w tym wybranym wcześniej
punkcie
5.przez punkty A' i B' prowadzimy dwie proste prostopadłe do tej symetralnej
6. proste prostopadłe z punktu 5 przetną ramiona kąta AOB w punktach A oraz B
wyznaczając bok dziesięciokąta
7. szukany promień R to odcinek łączący środek pierwotnie danego okręgu z wyznaczonymi w
punkcie 6 punktami.
Czy w punkcie 5 nie miało być równoległe do symetralnej (lub ewentualnie prostopadłe do A'B')
Wypróbuję twoją propozycję w geogebrze
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
Gdyby cię zapytano o uzasadnienie poprawności konstrukcji
i opisanie poszczególnych kroków konstrukcji z uwzględnieniem tego
dlaczego należy wykonać taki a nie inny ciąg kroków to co byś napisała
2 sty 09:23
Mariusz:
Wcześniej może za bardzo skupiłem się nad dokładnym odtworzeniem konstrukcji z obrazka
i dlatego mi nie pasowało to dowolne położenie odcinka A'B'
2 sty 09:29
Mariusz:
A nie jest dobrze ma być prostopadła do środkowej
2 sty 09:48
a7: 09:23 gdyby mnie zapytano o uzasadnienie poprawności konstrukcji, no to chyba bym powtarzała
masło maślane w kółko
bo skąd wiadomo, że podzielenie odcinka na pół jest poprawne? (to jeden z pierwszych kroków),
ta konstrukcja jest dość zdrowo rozsądkowa w moim rozumieniu. nie wiem, gdzie ktoś mógłby mi
kazać uzasadniać jej poprawność
czy możesz podesłać linka do przykładowego uzasadnienia konstrukcji o podobnym poziomie
trudności to
coś może spróbuję wymyślić
2 sty 09:50
a7: czyli ok?
2 sty 09:52
a7: z tymże tam jest błąd w nazewnictwie bo to nie jest symetralna a prosta prostopadła do
dwusiecznej
(już to poprawiałam)
2 sty 10:02
a7: a ok, widzę ze to zauważyłeś jednak 9:48
2 sty 10:04
Mariusz:
Właśnie sprawdziłem twoją propozycję i mimo iż różni się nieco od konstrukcji przedstawionej
na rysunku to daje poprawną konstrukcję dziesięciokąta o danej długości boku
Przykładowo aby uzasadnić poprawność konstrukcji odcinka
o długości będącej iloczynem bądź ilorazem długości dwóch danych odcinków
korzystasz z twierdzenia Talesa
Jeżeli chcesz uzasadnić poprawność konstrukcji odcinka będącego
pierwiastkiem kwadratowym z pewnej liczby korzystasz z podobieństwa trójkątów
Niech a > b ,
ponadto niech AB = a będzie średnicą pewnego okręgu
W punkcie P takim że AP=b prowadzisz prostopadłą do AB
Niech punkt C będzie przecięciem prostopadłej do AB w punkcie P
oraz okręgu o którego średnicą jest AB
Otrzymujesz dwa trójkąty podobne
Teraz aby uzasadnić że długość AC jest równa √ab
korzystasz z odpowiednich proporcji ułożonych z tych trójkątów podobnych
2 sty 10:27
a7: ale tu mamy dowolny pięciokąt wpisany w okrąg i dowolny bok AB dziesięciokąta i nie musimy
sie posługiwać pojęciami ilorazu/iloczynu(?)
2 sty 11:55
a7: ?
2 sty 12:14
ma pytanie: ok, znalazłam pdf, w którym sa uzasadnienia konstrukcji, spróbuję się im przyjrzeć i uzasadnić
tę "moją"
2 sty 13:39
a7: znalazłam pdf, w którym są uzasadnienia konstrukcji, spróbuję się im przyjrzeć i uzasadnić tę
"moją"
2 sty 13:40
Mariusz:
Skoro upraszczamy tę jego konstrukcję to nie musimy konstruować dwusiecznych bo
kąt 18° możemy dostać dopełniając kąt środkowy pięciokąta do kąta prostego
(Konstrukcja dwóch prostopadłych średnic jest etapem konstrukcji pięciokąta wpisanego w okrąg)
2 sty 13:55
a7: no ale wtedy nie będzie ramion kąta AOB i to będzie zupełnie co innego raczej
2 sty 14:09
a7: poza tym dopełnienia kata srodkowego pięciokata do kąta prostego też trzeba konstruować a
rysunek/konstrukcja robi się nieczytelny a przynajmniej mniej czytelny i wcale nie taki prosty
jak był (moim zdaniem)
2 sty 14:23
Mariusz:
Prowadzimy prostopadłą do OA przechodzącą przez O
Zaznaczamy punkt przecięcia tej prostopadłej i okręgu k
i mamy kąt 18° który w razie potrzeby możemy przenieść okręgiem w inne miejsce
Poza tym konstrukcje tych prostych prostopadłych dostajemy podczas
konstrukcji pięciokąta foremnego znanymi sposobami
2 sty 14:58
a7: możliwe..., ale nie rozumiem czy mam potwierdzić, że rozumiem Twoją konstrukcję? czy też jest
poprawna?
2 sty 15:14
a7: ja nie jestem jakąś specjalistką wielką, tylko ta wyjściowa chyba była bardziej intuicyjna...
2 sty 15:14
Mariusz:
Jakiś czas temu wyprowadziłem dwa sposoby konstrukcji wielokątów foremnych
o danej długości boku
Pierwszy sposób konstrukcji opierał się na konstrukcji trójkąta równoramiennego
gdzie kąty przy podstawie miały miarę równą połowie miary kąta wewnętrznego wielokąta
a kąt między ramionami był kątem środkowym wielokąta
(Dla pięciokąta foremnego kąt o mierze równej połowie miary kąta wewnętrznego można
dostać z wartości sinusa)
| | √5+1 | | | |
sin(54°)= |
| co można zapisać jako |
| |
| | 4 | | | |
czyli potrzebujemy zbudować taki trójkąt w którym przyprostokątna leżąca naprzeciw kąta
| | 1 | | √5−1 | |
jest równa |
| a a przeciwprostokątna jest równa |
| a , |
| | 2 | | 2 | |
gdzie a jest daną długością boku
| | √5−1 | |
Aby skonstruować odcinek |
| a konstruujemy trójkąt prostokątny |
| | 2 | |
| | 1 | |
o długościach boków a oraz |
| a wtedy z tw Pitagorasa długość przeciwprostokątnej |
| | 2 | |
tego trójkąta będzie równa ...
| | 1 | |
Następnie na jednym z końców tej przeciwprostokątnej rysujemy okrąg o promieniu |
| a |
| | 2 | |
i tak otrzymujemy kąt 54°
Drugi sposób to konstrukcja kąta zewnętrznego a następnie wyznaczenie środka okręgu
opisanego na wielokącie foremnym
Dla pięciokąta wyglądałoby to tak
| | √5−1 | | | |
Wiemy że cos(72°) = |
| co można zapisać jako |
| |
| | 4 | | | |
| | √5+1 | |
Konstrukcję odcinka |
| a |
| | 2 | |
można przeprowadzić analogicznie jak w przypadku pierwszej konstrukcji
Mając kąt zewnętrzny mamy także kąt wewnętrzny (są to kąty przyległe)
Niech wierzchołek kąta wewnętrznego będzie środkiem okręgu o promieniu a
dostajemy wtedy dwa boki wielokąta foremnego które są nierównoległymi cięciwami
okręgu opisanego na tym wielokącie więc środek okręgu wyznaczymy prowadząc
symetralne tych boków
Na powyższe konstrukcje sam wpadłem mając do dyspozycji tylko pomocnicze konstrukcje
znalezione w tablicach
2 sty 16:59
a7: może to powinieneś gdzieś opublikować? (poza forami)
2 sty 17:37
Mariusz:
W konstrukcjach które wyprowadziłem podwajanie liczby boków
odbywa się z wykorzystaniem twierdzenia o kątach wpisanym i środkowym
opartych na tym samym łuku
Obawiam się że te dwa sposoby konstrukcji są znane
więc publikacja nie ma sensu
2 sty 18:14
a7: rozumiem
2 sty 18:16


 ale jak zaczynamy rysować to mamy tylko okrąg z pieciokatem z katem AOB oraz z odcinkiem
AB wolnym
ale jak zaczynamy rysować to mamy tylko okrąg z pieciokatem z katem AOB oraz z odcinkiem
AB wolnym
 środek odcinka AB wyznaczamy na zadanym odcinku potem go nanosimy połowami na symetralną
dwusiecznej AOB
(autor rysunku ma na rysunku punkty A oraz B dlatego ja te oznaczające bok dziesięciokąta
pogrubiam {P[A]] oraz {P[B]]
środek odcinka AB wyznaczamy na zadanym odcinku potem go nanosimy połowami na symetralną
dwusiecznej AOB
(autor rysunku ma na rysunku punkty A oraz B dlatego ja te oznaczające bok dziesięciokąta
pogrubiam {P[A]] oraz {P[B]]
 1. wyznaczamy punkt B
2. wyznaczamy dwusieczną (zwaną w pierwotnym rysunku środkową kata AOB)
3. dzielimy dany odcinek AB na pół
1. wyznaczamy punkt B
2. wyznaczamy dwusieczną (zwaną w pierwotnym rysunku środkową kata AOB)
3. dzielimy dany odcinek AB na pół
 4. na dwusiecznej wybieramy (dowolonie punkt, do którego kreslimy prosta prostopadłą)
5. na tę prostą prostopadłą nanosimy połówki odcinka AB
6. kreślimy proste prostopadłe do niebieskiej prostopadłej do dwusiecznej i one wyznaczają nam
punkty A oraz B
7. zrobione
4. na dwusiecznej wybieramy (dowolonie punkt, do którego kreslimy prosta prostopadłą)
5. na tę prostą prostopadłą nanosimy połówki odcinka AB
6. kreślimy proste prostopadłe do niebieskiej prostopadłej do dwusiecznej i one wyznaczają nam
punkty A oraz B
7. zrobione 