Układ równań z wartością bezwzględną yn: Jak obliczyć taki układ równań: { |x|−y=1 { −x+|y|=1

wredulus_pospolitus: 1) niech x≥0 x−y=1 −−−> x = 1+y −x + |y| = 1 −−−> −1 − y + |y| = 1 −−−> |y| − y = 2 −−−> może być spełnione tylko gdy y<0 ... a wtedy −y − y = 2 −−−> y = −1 a to ciągnie za sobą: x = 0 2) niech x<0 −x − y = 1 −−−> −x = 1+y −x + |y| = 1 −−−> 1+y + |y| = 1 −−−> y + |y| = 0 −−−> albo y = 0 albo y < 0 ... bo wtedy y − y = 0 dla y=0 mamy x = −1 dla y<0 mamy x = |y| − 1 ... zauważmy, że mamy warunek x<0 ... więc |y| < 1 więc y∊(−1 ; 0) a wtedy x = −y − 1 (czyli nieskończenie wiele rozwiązań

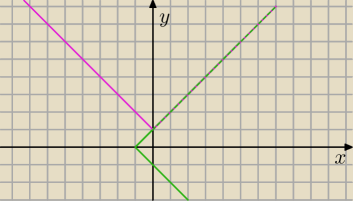
chichi: Graficznie (I) y = |x| + 1 (II) x = |y| − 1 − spójrz na układ w drugą stronę i rysuj jakobyś 'x' zamienił z 'y'

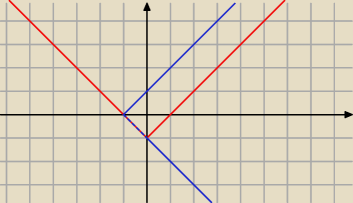
wredulus_pospolitus: drugi sposób: granicznie. |x| − y = 1 −−−> y = |x| − 1 −x + |y| = 1 −−−> x = |y| − 1 i bierzesz część wspólną czyli wszystkie punkty na odcinku AB, gdzie A (−1,0) , B (0,−1)

wredulus_pospolitus: @chichi ... fioletowa funkcja źle

chichi: Ehh.. nie zmieniłem znaku w 1 równaniu, wykres powinien wyglądać jak u @wredulus