kwadrat
Martunia:
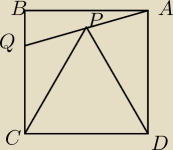
DCP jest trójkątem równobocznym wenątrz kwadratu ABCD (rys). AP przecicina bok BC w Q. Uzasdij
że można wybrać punkt R na CD tak że AQR będzie trójkątem równobocznym.
28 gru 19:48
Eta:
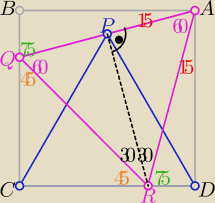
28 gru 20:57
28 gru 21:31
kerajs:
Te grafiki są zarówno życzeniowe, jak i nieprawdziwe. Jeśli trójkąty AQR i CDP są równoboczne
to P nie leży na odcinku AQ .
29 gru 21:16
kerajs:
A nie, to ja się pomyliłem. Faktycznie P jest środkiem AQ.
29 gru 23:08
chichi:
A drugie zadania dla @
Ety czeka i czeka...
29 gru 23:21
a7: wyznaczyłam boki trójkątów CTR i DSA z tw. sinusów i wpisałam do wolframa, ale wychodzi, że to
nie jest prawda
31 gru 04:17
a7: z obliczeń na piechotę zresztą też nie wyszło...
31 gru 04:19
a7: tzn. mam na myśli że r1=2r2
31 gru 04:42
an: Rysunek w GEOGEBRA potwierdza r1=r2, gdzieś się pomyliłeś
31 gru 10:18
an: r1=2r2
31 gru 10:20
chichi:
No to wstaw ten rysunek z GeoGebry
31 gru 11:31
a7: o właśnie
31 gru 11:31
a7: ja zaraz pokażę obliczenia może ktoś wychwyci błąd
31 gru 11:36
chichi:
@
a7 Ułatwmy nie co zadanie, przyjmijmy, że bok kwadratu wynosi 1, sprawdź teraz czy działa
31 gru 11:37
a7: r
MNIEJSZY=2P
2/(a+b
2+c
2)
R
WIĘKSZY=2P
1/(a−x+b
1+c
1)
| a−x | | b1 | | c1 | |
| = |
| = |
| |
| sin75 | | sin45 | | sin60 | |
| a | | b2 | | c2 | |
| = |
| = |
| |
| sin135 | | sin15 | | sin30 | |
| | 2*1/2*a*sin15/cos45*asin30/cos45*sin30 | |
r= |
| |
| | a+asin15/cos45+asin30cos45 | |
| | 2*1/2*(a−x)*sin45/sin755*(a−x)sin60/sin75 | |
R= |
| |
| | a−x+(a−x)sin45/sin75+(a−x)sin60/sin75 | |
31 gru 11:46
a7: przy r w mianowniku brakuje / przy asin30/cos45
31 gru 11:47
a7: 11:37 ok
31 gru 11:47
a7: | | sin15 | |
jeszcze poprawka a−x=a−a* |
| |
| | sin75 | |
31 gru 11:48
a7: przy R w liczniku brakuje pomnożenia przez sin75 czyli *sin75
31 gru 11:49
31 gru 11:51
31 gru 11:55
a7: wyszło
31 gru 11:55
a7: dzięki za pomoc
31 gru 12:02
a7: dobra na piechotę chyba też już mam
31 gru 12:07
chichi:
No i super, ja wciąż czekam na rysunek od @
an
31 gru 12:48
