próbna matura Michał: czy mógłby mi ktoś pomóc w rozwiązywaniu testu maturalnego? zadanie1. Wartość wyrażenia W=³√16−2√50+4√32−³√250 jest równa: A 2³√4+6√2−5³√10 B −3³√2+6√2 C 2³√4−26√2−5³√10 D −3³√2−26√2 zadanie2. Liczba 120 jest o 50% większa od liczby x, wynika stąd że: A x=200 B x=180 C x=80 D x=60 zadanie3. Jeśli log₂ 7=a, to liczba log₂ 56 jest równa: A 8a B a+8 C 3a D a+3 zadanie4.

	9x2−16y2
Jeżeli		=25 to:
	3x−4y

A 3x+4y=25 B 3x−4y=25 C 3x+4y=5 D 3x−4y=5 zadanie5. Sześcian liczby 2+√3 jest równy: A 7 B 15√3+26 C 11 D 35+12√7 zadanie6. Zosia czyta k stron w ciągu m godzin. wynika stąd że w ciągu m+5 godzin przeczyta stron:

	k(m+5)		5m		k		k+5
A		B		C		+5 D
	m		k		m		m

zadanie7. Jeżeli 2x−5=√3x−1 to:

	4		−6		4		−6
A x=		B x=		C x=		D x=
	2√3		2√3		2−√3		2−√3

zadanie8.

	(2x+3)2
Wyrażenie W=		po skróceniu ma postać:
	(4x2−9)2

	1		1		1		1
A		B		C		D
	2x−3		2x+3		(2x+3)2		(2x−3)2

zadanie9. Równanie x²−6x+c=0 nie ma rozwiązania gdy: A c∊(9;+∞) B c∊<9,+∞) C c∊(−∞,9) D c∊(−∞,9> zadanie10. zbiorem rozwiązań nierówności 16−x²>0 jest: A (−∞;4) B (4;+∞) C (−4;+4) D (−∞;−4)∪(4;+∞) zadanie11. Suma ciągu ayrtm. jest okreslona wzorem S_n =3n²+6n. drugi wyraz tego ciągu jest równy: A 24 B 15 C 6 D 2 zadanie12. pierwszy wyraz ciągu arytm. jest równy log₅ 3, a drugi wyraz log₅ 15. różnica tego ciągu to liczba: A log₅ 45 B log₅ 12 C 12 D 1 zadanie13.

	1
Ciąg (log2		,x,−1) jest geometryczny. wynika z tego, że:
	16

	1		1		1		1
A x=−		B x=		C x=−		⋁ x=		D x=−2 ⋁ x=2
	16		16		4		4

zadanie 14. nieprawdą jest że: A sin25st<sin34st B tg2st<tg64st C cos15st<cos24st D cos23st>cos44st zadanie15.

	√3
prosta o równaniu y=		x+1 jest nachylona do osi OX pod kątem α takim, że:
	3

A α=30st B α45st C α=60st D α>60st zadanie16. stosunek długości podstawy do ramienia trójkąta równoramiennego jest równy 2:3. ramię jest nachylone do podstawy pod kątem α takim, że:

	2√2		2		1		2√2
A cosα=		B cosα=		C sinα=		D sin=
	3		3		3		3

zadanie17. w trójkącie jeden z kątów jest o 20st większy od najmniejszego, a trzeci kąt jest trzykrotnie większy od najmniejszego. najmniejszy z kątów tego trójkąta ma miarę: A 7,5st B 32st C 40st D 54st zadanie18. dany jest trójkąt ABC o kącie 80st przy wierzchołku C. kąt między dwusieczną tego kąta a wysokością poprowadzoną z wierzchołka C ma miarę 15st. wynika stąd że kąt ABC jest równy: A 15st B 35st C 75st D 105st zadanie19. Wysokość trójkąta prostokątnego poprowadzona z wierzchołka kąta prostego ma długość 4. wysokość ta dzieli przeciwprostokątną na dwa odcinki z których jeden ma długośc 2. przeciwprostokątna jest równa: A 4√3 B 4√5 C 8 D 10 zadanie20. z przeciwległych wierzchołków kwadratu o boku 1 zatoczono koła o promieniu 1. pole części wspólnej tych kół jest równe:

	1		1		1		1
A		π B		π C		(π−2) D		(π−2)
	4		2		4		2

zadanie21. suma miasr kątów wewnętrznych wielokąta wypukłego jest równa 1800st. wynika stąd że liczba boków tego wielokąta jest równa: A 5 B 7 C 10 D 12

Julek: Mniej czasu zajęłoby Ci rozwiązanie tych zadań niż przepisywanie

Michał: to fakt, sam się nad tym zastanawiałem, tyle że spośród nich potrafię zrobić nie wiele

Godzio: napisz ktore nie umiesz a z reszta się pomoze

Godzio: napisz ktore nie umiesz to się pomoze

Mickej: wszystkie inaczej by nie wpisywał

Eta:

Michał: 3, 4, w 5 muszę te wyrażenie wziąć w nawias podnieść do potegi 3 i obliczyć według wzrosu skróconego mnożenia?, 6, 9, 10, ciągi czyli od 11 do 13, nie wiem o co chodzi w 14, 17, 18, 19, 20, 21

Eta: 3/ log₂56= log₂7*8= log₂7+log₂8= log₂7+3= a+3 odp: D)

Eta: 10/ log₂¹₁₆= −4 ciąg −4, x, −1 −−− geometryczny => x²= (−4)*(−1) x²=4 => x = 2 v x= −2 odp; D)

Godzio: 3. log₂56 = log₂7 + log₂8 = a + 3 4.

9x2−16y2
	= 25
3x−4y

(3x−4y)(3x+4y)
	= 25
3x−4y

3x + 4y = 25 5. (2+√3)³ = rozpisz wg wzoru skróconego mnożenia 6. m − k m+5 − x

	k(m+5)
x =		A
	m

9. x²−6x+c=0 zał. Δ < 0 Δ=36 − 4c < 0 36 < 4c c > 9 c∊(9,∞) 10. 16−x² > 0 x² < 16 x<4 i x>−4 x∊(−4,4) zaraz reszta

Godzio: Eta chyba pomyliłaś numer zadanka

Eta: No tak zad. 13 ......... pechowa "13"−tka

Godzio: jeśli nie rozumiesz ciągów to proponuje poczytać tutaj : https://matematykaszkolna.pl/strona/i12.html

Eta: z tylu zadań , oczopląsu można dostać

Godzio: 12. a₂ = a₁ +r log₅3 − log₅15 = r

	3
log5		= r
	15

r = log₅5⁻¹ r = −1 i tam w odpowiedzi D zdaje się że miało być −1 prawda ?

Godzio: no dokładnie

Godzio: 14. narysuje sobie wykres i sprawdzaj 17. α, α+20, 3α => 3 kąty trójkąta α + α+20 + 3α = 180 α = ...

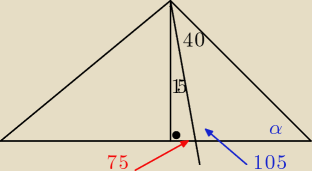
Godzio: α = 180 − 105 − 40 = 35

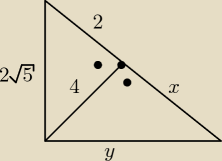
Godzio: 4² + x² = y² 2√5² + y² = (2+x)² 20 + 16 + x² = 4 + 4x + x² 32 = 4x x = 8 2+x = 10

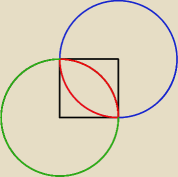
Godzio: Pole tego kawałka kwadratu który nie wchodzi w część wspólną oznaczymy P_k P_w − pole wycinka koła o kącie 90^o

	1
Pk = Pkw. − Pw = 1 −		π
	4

	1		1		1		1
Pcz. wsp. = Pw − Pk =		π − 1 +		π =		π −1 =		(π−2)
	4		4		2		2

Godzio: n = 12

Godzio: do zad 21 n = 12

Michał: to 2+x=10 i ten cały rysunek to do któregom zadania?

Michał: α = 180 − 105 − 40 = 35 a to do którego jest?

Michał: co dalej z zadaniem 14? mam pytanie do zadanie 17 czyli wyszło mi 32st? a w zadaniu 18 35st?

Michał: proszę jeszcze o zadania 11 i 19

Godzio: 14. mowilem wez sobie dowolny wykres sin, cos, tg i sprawdzaj po wykresie czy wartosci odpowiadajace danym kątom są większe od siebie czy mniejsze 17. α, α+20, 3α => 3 kąty trójkąta α + α+20 + 3α = 180 α = 32 pisałem już ... 18. tez juz pisalem i odp 35

Godzio: 19 tez zrobione 5marca 16:33

Michał: b. dziękuję

Michał: czy w czternastym będzie B?

Przemek: A mógłbym ktoś wytłumaczyć mi jak zrobić zadanie 1

gosc: a 15

marta: te wszystkie zadania tutaj są źle zrobione. Dziś prawie wszystkie zrobiłam i jakoś inne wyniki miałam i sprawdzałam te zadania z panią korepetytor

Mila: Martusiu nie wierzę. Zaraz sprawdzam.

Justyna: HEllo ! czy ktokolwiek mógłby mi powiedzieć z którego roku jest ten zestaw arkuszy maturalnych ?proooszę o pomoc