Rozwiązać równanie |x+1|-|x-1|=5.
PIT: Czy równanie nie ma żadnych rozwiązań, czy ma jedno w przypadku, gdy:
x+1<0,
x−1>=0, to x∊(−∞,−1)v<1,+∞)
−(x+1)−(x−1)=5,
−x−1−x+1=5,
−2x=5,
x=−5/2 !?
26 gru 22:42
Eta: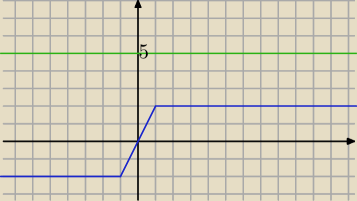f(x)=|x−1|−|x+1|
g(x)=5
równanie sprzeczne
26 gru 22:49
Mila:
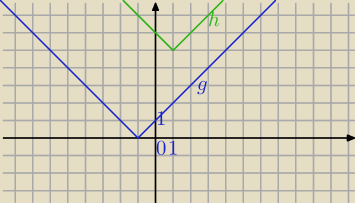
II sposób
|x+1|=5+|x−1|
g(x)=|x+1|
f(x)=5+|x−1|
Brak rozwiązań.
Jeszcze małe uzasadnienie. Napiszesz?
f(x)=|x−1|−|x+1|
g(x)=5
równanie sprzeczne
II sposób
|x+1|=5+|x−1|
g(x)=|x+1|
f(x)=5+|x−1|
Brak rozwiązań.
Jeszcze małe uzasadnienie. Napiszesz?