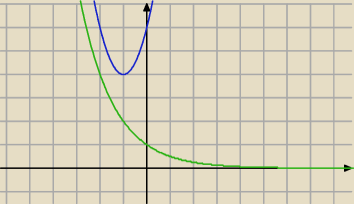
Czy istnieje punkt wspólny wykresów funkcji versager: Czy istnieje punkt wspólny wykresów funkcji: a) kwadratowej 2x² + 4x + 6, b) wykładniczej 2⁻x; jeśli tak, podaj jego współrzędne czy macie jakis pomysl? kombinowalem i kombinowalem, ale wychodzi na to, ze to bedzie cos dziwnego

a7:

a7:

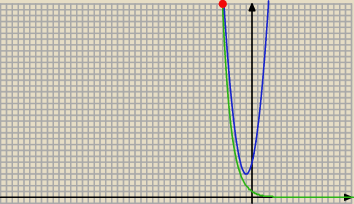
versager: masz racje, jest to x≈−5.44129 ale czy da sie to okreslic dokladniej? typu jakis logarytm czy inna funkcja

a7: dla x=−5 2x²+4x+6=50−20+6=36 1/2⁻⁵=32

a7: zaraz sprawdzę w wolframie

a7: chyba już sprawdzałeś w wolframie? tu może trzeba jakiegoś triku... nie wiem

versager: tak, sprawdzalem, tez wlasnie myslalem o triku, probowalem wyizolowac to 2 i przedstawic je za pomoca logarytmu czy cos no ale lipa najwyrazniej nie da wyrazic rozwiazania za pomoca funkcji elementarnych, niemniej jednak dziekuje za rozwianie watpliwosci

a7: może jeszcze ktoś zabierze głos i coś wymysli

versager: dobrze by bylo

a7: a masz odpowiedź z podręcznika/notatek itp.

a7: ?

versager: nie, to zadanie dostalem od znajomego i tyle tak naprawde

sagro: po przekształceniach równania za pomocą dania log o podst. 2 z obu stron i potem użycia def log można dojść do postaci 2^−(x+1) = (x+1)² + 2. Równania typu y^x = x^y (tutaj y = 2, x = (x+1)) można rozwiązać za pomocą funkcji W Lamberta (wyniki przybliżone i tak otrzymujemy za pomocą kalkulatora złożonego) tutaj podsyłam filmik z wytłumaczeniem https://www.youtube.com/watch?v=ZVnW6WAM_Co Natomiast wszystko psuje te + 2 i niestety nie wiem jak to rozwiązać. Może kogoś naprowadziłem na pomysł.

versager: dziekuje