Wzór Herona Algorytm: Mając wzór na promień okręgu wpisanego, a mianowicie:

	PΔ
r =
	p

Gdzie: − PΔ − pole trójkąta − p − połowa obwodu trójkąta Wyprowadziłem z tego wzór na Pole trójkąta: PΔ = r * p, lecz gdy obliczam za pomocą tego wzoru to mam inny wynik w porównaniu do wzoru Herona: √p(p−a)(p−b)(p−c) Dlaczego tak jest? a = 4x, b = 6x, c = 8x A r = √7

	15√7x
Wynik ze wzoru PΔ = r * p otrzymuję		, ale przy używaniu wzoru Herona otrzymuję:
	2

15√7x2
4

Dlaczego?

Algorytm: Znaczy a = 4x b = 5x c = 6x

chichi: Bo 'x' również powinien występować w 'r' bo bzdurą jest, że promień okregu jest wielkością stałą, gdy w tym przypadku sparametryzowane są długości boków tego trójkąta, co jak wezmę x=1 to długość promień okregu wpisanego w ten trójkąt wówczas o bokach (4,5,6) jest równa √7, a jak wezmę x = 1000 to wówczas mam trójkąt o bokach (4000, 5000, 6000) i długość promienia okręgu wpisanego w ten trójkąt też będzie równa √7? No zastanów się

Algorytm: No okej, a wtedy co mam zrobić z mianownikiem?

chichi: Pisz konkretnie, bo nie wiem, o który mianownik chodzi.

	P		3.75√7x2
r =		=		= 0.5√7x − tyle wynosi promień
	p		7.5x

Algorytm: Ahaaaaaaa, a dlaczego tak to robimy, a nie możemy dodać do promienia x? Znaczy nie do końca rozumiem jak to jest XD

Algorytm: I skąd mamy 3.75√7x²? O Bożeeeeeeeee tyle pytań XDDDDDDD

chichi:

15
	= 3.75, zapisałem w ułamku dziesiętnym.
4

Z jakiej racji mamy dodać 'x' do 'promienia'?

	P
r =		, gdzie P = 3.75√7x2, a p = 7.5x, sam zapisałeś ten wzór
	p

Algorytm: No tak, ale dylemat jest taki, że na początku nie wiemy jakie jest pole, lecz mamy jedyne dane to promień i boki.

	P
Więc jak mogę użyć ten wzór P = r * p, skoro musimy obliczyć r =
	p

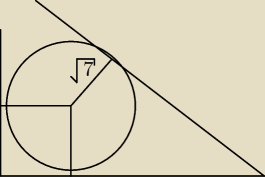
a7: promień masz dany (√7) nie uzależniony od x czyli możesz wyliczyć x

chichi: No to mając boki masz i promień możesz policzyć na minimum 2 sposoby: (1) Wzór Herona

	L
(2) P = pr, gdzie p =
	2

A to, że ktoś Ci podał błędną długość promienia to masz różne wyniki, ja przy użyciu wzoru Herona pokazałem jakiej postaci powinna być ta prawidłowa dłg promienia

a7: chichi wyliczył, że r=0,5√7x czyli √7=0,5*√7x czyli x=2

chichi: A teraz możesz znaleźć sobie 'x' jak pisze @a7 przyrównać 0.5√7x = √7 i masz x = 2, teraz możesz wyliczyć sobie pole czy co tam chcesz wstawiając odpowiednio x = 2

a7: no właśnie wszystko się zgadza

Algorytm: No na wzór Herona to tak. Ale nadal nie rozumiem, mając dane, że a = 4x b = 5x c = 6x I wiedząc, że Pole kołą równa się 7Pi, to obliczyłem za pomocą tego r, że r = √7

	15x
Teraz obliczę p =
	2

Ale teraz nie rozumiem, skoro mamy nie znane P, to jak podstawie to p * r, to nie wyjdzie nam

15√7x2
4

Chodzi mi o to, że jak mogliśmy obliczyć Pole, nie znając r z x?

a7: czyli wracając do twojego pierwotnego pytania

15√7x		15√7x2
	=		gdyż x=2
2		4

a7: może daj pierwotną treść zadania, bo trudno zrozumieć o co Ci chodzi?

Algorytm:

	1
Nie dociera do mnie, jak otrzymaliśmy		√7x nie wiedząc, czym jest pole? xd
	2

(Żeby obliczyć to pole prawidłowo, to musimy mieć r z x'em, nie?), a mamy r jako P{7}

Algorytm: Treść zadania jest taka: W trójkącie stosunek długości boków wynosi 4 : 5 : 6. Oblicz pole tego trójkąta oraz r koła opisanego na tym trójkącie, wiedząć, że pole koła wpisanego w ten trójkąt wynosi 7Pi

chichi:

	4x+5x+6x
Nie bo do wzoru Herona nie potrzebujemy promienia, mam że p =		= 7.5x
	2

P = √7.5x(7.5x−4x)(7.5x−5x)(7.5x−6x) = 3.75x²

	P		3.75x2
r = √7 ∧ r =		=		= 0.5√7x ⇒ √7 = 0.√7x ⇒ x = 2
	p		7.5x

Algorytm:

	1
No bo nie rozumiem, jak możemy obliczyć promień z x (To co wam wyszło		√7x), nie
	2

znając,

	15√7x2
że Pole trójkąta =
	4

	15x
Wiem tylko, że r = √7 i p =		.
	2

Nie mam pojęcia jak obliczyliśmy promień z x, gdy używamy do jego obliczenia prawidłowe

	15√7x2
pole, którego nie znamy (		)
	4

Algorytm: No tak, to przez wzór Herona, ale jak to zrobić nie używając go? xd

chichi: Zatem P = 3.75*2² = 15, a = 4x = 8, b = 5x = 10, c = 6x = 12

	abc		8*10*12
R =		=		= 16
	4P		4*15

Algorytm: Da się obliczyć pole z takimi danymi bez używania wzoru Herona?

chichi: Czytaj 13:07

Algorytm: No okej, na 13:07 używamy wzoru Herona do obliczenia pola, a da się go obliczyć innym sposobem?

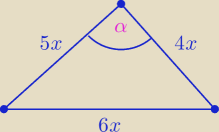
chichi: Da się np. tak: Tw. Carnota: (6x)² = (5x)²+(4x)²−2*4x*5x*cos(α) ⇔ 36x² = 25x²+16x²−40x²cos(α) ⇔

	1		3√7
cos(α) =		⇒ sin(α) =
	8		8

	1		3√7
⇒ P =		*4x*5x*		= 3.75√7x2
	2		8