Przekroje. Marina : W ostrosłupie prawidłowym trójkątnym poprowadzono przekrój płaszczyzną zawierającą krawędź podstawy i prostopadła do przeciwległej krawędzi bocznej. Wiedząc, że kąt między dwiema sąsiednimi krawędziami bocznymi ma miarę 2*alfa, gdzie alfa należy (0°, 45°), oblicz: A) cosinus kąta beta przy wierzchołku przekroju należącym do krawędzi bocznej, B) cosinus kąta gamma nachylenia płaszczyzny przekroju do płaszczyzny podstawy ostrosłupa. Proszę o pomoc.

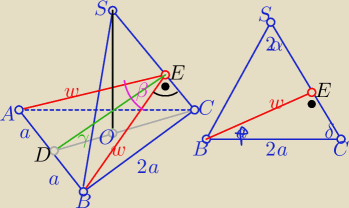
Eta: |DC|=a√3 B|=2a w ΔBCS δ= 90^o−α ⇒ φ=α to w ΔBEC w=2acosα z tw. cosinusów w ΔABE

	w2+w2−4a2		2cos2α−1
cosβ=		⇒ cosβ=
	2w2		2cos2α

	cos(2α)
cosβ=
	cos(2α)+1

===============

	|DE|
w ΔDCE cosγ=		|DE|=√w2−a2 =...... =a√4cos2α−1
	|DC|

	√3
to cosγ=		√4cos2α−1
	3

=================

Eta: Oczywiście ma być: |AB|=2a

Eta: I jeszcze dla jasności Δ DEC prostokątny bo |∡DEC|=90^o

Eta: