Oblicz ekstrema funkcji Vander: y=x+√1−x

	1		1+2√1−x
pochodna = 1+		=
	2√1−x		2√1−x

1+2√1−x
	=0 −1≠2√1−x
2√1−x

nie wiem czy dobrze to policzyłem ale funkcja ta nie ma ekstremum ?

wredulus_pospolitus: brak pochodnej wnętrza w drugim członie funkcji

Vander: możesz tak bardziej łopatologicznie ?

I'm back: Pochodną we wnętrza z wyrażenia √1−x nie została policzona. Co tutaj jest (w tym wyrażeniu) funkcja wewnętrzna?

janek191:

	−1
y ' = 1 +
	2√1 −x

janek191:

Vander: funkcją wewnetrzną jest 1−x ?

janek191: Tak

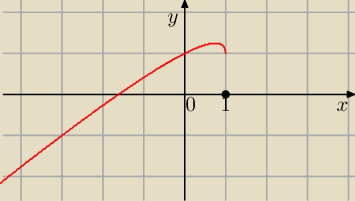
wredulus_pospolitus: Przy okazji drogi studencie. Warto czasem popatrzeć na samą funkcję zauważ, że f(0) = 0 + √1 = 1 ; f(1) = 1 + √0 = 1 mamy dwie takie same wartości funkcji ... więc o ile nie jest to funkcja stała lub nie jest ciągła w przedziale (0,1) (a nie jest ani taka ani taka) to musi być jakieś ekstremum w przedziale (0,1)

wredulus_pospolitus: a pochodna z niej to jest (−1) i stąd ten minus w liczniku i stąd 'pojawia się nam' ekstremum

Vander: Dzięki wielkie za wytłumaczenie po 5 latach przerwy od matmy ciężko się kuma nawet takie podstawy