Zbadaj liczbę rozwiązań równania.
frogskullnbones:
Witam,
mam problem z rozwiązaniem równania:
|x
2 + x − 30| = (m −
32)|x − 5|
Należy zbadać liczbę rozwiązań w zależności od parametru m.
Proszę o pomoc, nie mam pojęcia jak to zrobić.

16 gru 22:20
janek191:
x2 + x − 30 = ( x + 6)*(x − 5) więc
I x2 + x − 30 I = I x + 6 I*I x − 5 I
itd.
16 gru 22:26
frogskullnbones: niestety nie wychodzi poprawnie
16 gru 22:27
b4:
wskazówka
|x2+x−30|=|x+6|*|x−5|
16 gru 22:27
frogskullnbones: mógłby mi ktoś wytłumaczyć, ponieważ nadal nie wiem skąd wyznaczyć liczby rozwiązań
16 gru 22:30
ABC: to równanie zawsze ma jedno rozwiązanie x=5 niezależnie od wartości m , bo uzyskujesz wtedy 0=0
następnie podziel obie strony przez |x−5| przy założeniu x≠5 i badaj dalej
16 gru 22:39
frogskullnbones: w zadaniu muszę podać:
1. najmniejsze możliwe m, dla którego równanie ma 2 rozwiązania
2. największe możliwe m, dla którego równanie ma 2 rozwiązania
3. m, dla którego równanie ma 3 rozwiązania
4. m, dla którego ilość rozwiązań dodatnich jest równa ilości rozwiązań ujemnych.
Z moich obliczeń wynika, że to równanie nigdy nie będzie miało 3 rozwiązań, ani największego m
dla 2 rozwiązań.
16 gru 22:46
a7:
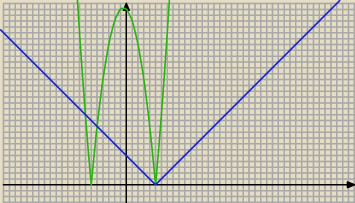
1. m=3/2 bo wtedy niebieski wykres jest równy 0 y=0
16 gru 22:51
a7:
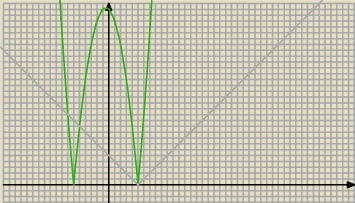
2. m=3/2 (?)
16 gru 22:54
a7: odpowiedź na (1) i (2) jest ta sama bo najmniejsze m jest jednocześnie największym m
16 gru 22:56
a7:
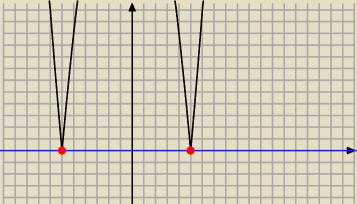
16 gru 22:56
a7: 3. a co powinno wyjść, to będzie mi łatwiej
16 gru 22:57
a7: ?
16 gru 22:57
a7: czy w 3 i 4 wystarczy podać przykładowe m?
16 gru 22:58
frogskullnbones: właśnie nie mam odpowiedzi, w 3 jest napisane, aby odpowiedź przedstawić w postaci sumy
przedziałów
16 gru 23:00
a7: ok
16 gru 23:00
ABC: "Z moich obliczeń wynika, że to równanie nigdy nie będzie miało 3 rozwiązań, ani największego m
dla 2 rozwiązań"
m=2,5
|x
2+x−30|=|x−5|
x=−7 x=−5 x=5 3 rozwiązania sprawdź jeśli nie wierzysz

słabe twoje obliczenia ...
16 gru 23:01
a7:
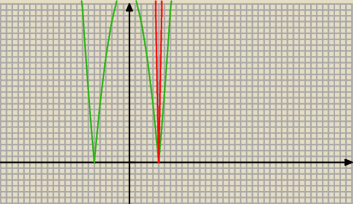
no to widzimy, że gdy m−3/2<0 to równanie ma jedno rozwiązanie x=5 czyli
dla m<3/2 (m∊(−
∞;3/2) jedno rozwiązanie (x=5)
dla m=3/2 dwa rozwiązania (x=5 lub x=−6)
teraz np.dla m−3/2=50 znowu jedno rozwiązanie
16 gru 23:08
a7: trzeba popatrzeć na wykresy i coś zauważyć albo jakoś inaczej algebraicznie podejść co zaraz
uczynię
16 gru 23:09
a7: |(x−5)(x+6)| − (m−3/2)|x−5|=0
|x−5|(|x+6|−(m−3/2))=0
x=5 lub
dla x+6≥0 czyli dla x≥−6
x+6−m+3/2=0
x=m−7,5
dla x−6<0
−x−6−m+3/2=0
x=−m−4,5
coś wyszło, ale nie wiem co dalej
16 gru 23:16
a7: chyba wiem
16 gru 23:17
ABC: dałem mu wskazówkę o 22:39 , po podzieleniu to jest klasyczne równanie
| | 3 | | 3 | | 3 | |
które ma dwa rozwiązania dla m> |
| , jedno dla m= |
| , zero dla m< |
| |
| | 2 | | 2 | | 2 | |
16 gru 23:20
a7: drugi przypadek napisałam błędnie x+6<0 czyli x<−6
16 gru 23:21
a7: no ale to równanie ma też czasem przecież trzy rozwiązania
16 gru 23:21
frogskullnbones: wydaje mi się, że dla m większego od 3/2 zawsze będą 3 rozwiązania
16 gru 23:25
a7: nic nie kumam
16 gru 23:27
a7: no tak by wynikało z tego co napisał ABC
16 gru 23:27
ABC: no i dobrze ci się wydaje, miło że włączyłeś myślenie
16 gru 23:27
ABC: aczkolwiek jest tam jeszcze klasyczna mała pułapka...
16 gru 23:28
a7: czy ja mam aż tak męski nick, bo ostatnio Mariusz też do mnie w formach meskich pisał,
chyba tylko Eta i Mila wiedzą, 'żem jest "oną"' (skoro już używamy anarchizmów
dzisiaj zamiast śpiulkolotów, które podobno są takie modne)
16 gru 23:32
a7: no i gdzie ta klasyczna pułapka? czy będzie nam dane się tego jeszcze Roku Pańskiego (Anno
Domini) 2021 dowiedzieć?
16 gru 23:35
ABC: teraz to nic nie wiadomo , kobieta to co innego, osoba z macicą to co innego

16 gru 23:36
a7: 23:08 dla m−3/2=50 jednak wciąż trzy rozwiązania
16 gru 23:36
a7: no ja to sobie tłumaczyłam, że może pisał do mnie per on czyli (ten) użytkownik forum
jakielkowliek płci by nie był, ale byłam zdziwiona, bo kilka razy z nim chyba wymieniłam parę
zdań o ile pamiętam i myślałam że jest na tyle spostrzegawczy, że nawet w tym poście też
używałam form żeńskich pisząc o swoich obliczeniowych "dokonaniach"
16 gru 23:39
frogskullnbones: w punkcie 4. chyba jest tylko jeden przypadek, gdy m=3/2, ponieważ tylko wtedy jest parzysta
ilość rozwiązań
16 gru 23:39
a7: no chyba tak
16 gru 23:39
a7: no dobra, to rozwiązane....
tylko gdzie ta pułapka?
16 gru 23:40
frogskullnbones: dziękuję bardzo za pomoc
16 gru 23:40
ABC: pułapka jest na przykład dla m=12,5
wtedy podzielone równanie |x+6|=11 ma jedno z rozwiązań 5 pokrywające się z tym które jest
zawsze
więc są tylko 2 rozwiązania
16 gru 23:41
b4:

16 gru 23:41
a7: hmmm, no tak....
16 gru 23:42
a7: 
16 gru 23:43
a7: 23:41 jeszcze podejrzane jest słowo/zwrot "na przykład" czy byłoby możliwe wyjaśnienie, gdzie
jeszcze jest ewentualna pułapka?
16 gru 23:49
ABC: zbadaj sama czy jest jeszcze jedna taka wartość parametru, gdzie mogą się pokryć

16 gru 23:51
a7: ech , no nic nie wiem, nie mam pomysłu, no nic pozostaje mi pozostać w niewiedzy, ale i tk jest
postęp

17 gru 00:01
Mila:
a7, algebraicznie próbowałaś?
Jutro spróbuję rozwiązać, mało jest zadań na forum to nie włączam
się do rozwiązywania, aby nie robić tłoku.
Pozdrawiam

17 gru 00:46
a7: 23:16 to była moja próba, ale niestety, nie do końca wyszło....
17 gru 00:53
a7: Pozdrawiam również

17 gru 01:22

 1. m=3/2 bo wtedy niebieski wykres jest równy 0 y=0
1. m=3/2 bo wtedy niebieski wykres jest równy 0 y=0
 2. m=3/2 (?)
2. m=3/2 (?)

 słabe twoje obliczenia ...
słabe twoje obliczenia ...
 no to widzimy, że gdy m−3/2<0 to równanie ma jedno rozwiązanie x=5 czyli
dla m<3/2 (m∊(−∞;3/2) jedno rozwiązanie (x=5)
dla m=3/2 dwa rozwiązania (x=5 lub x=−6)
teraz np.dla m−3/2=50 znowu jedno rozwiązanie
no to widzimy, że gdy m−3/2<0 to równanie ma jedno rozwiązanie x=5 czyli
dla m<3/2 (m∊(−∞;3/2) jedno rozwiązanie (x=5)
dla m=3/2 dwa rozwiązania (x=5 lub x=−6)
teraz np.dla m−3/2=50 znowu jedno rozwiązanie






