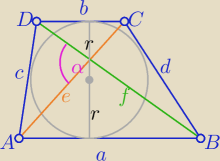
 c≥2r
d≥2r
to c+d≥4r i z warunku wpisania okręgu w trapez c+d=a+b
zatem a+b≥4r
2P=(a+b)*2r i 2P=efsinα dla α=90o pole jest największe
więc ef ≥ (a+b)*2r = 8r2 oraz e2+f2≥ 2ef
to mamy tezę:
|AC|2+|BD|2≥16r2
♣♣♣♣♣♣♣♣♣♣♣♣♣
c≥2r
d≥2r
to c+d≥4r i z warunku wpisania okręgu w trapez c+d=a+b
zatem a+b≥4r
2P=(a+b)*2r i 2P=efsinα dla α=90o pole jest największe
więc ef ≥ (a+b)*2r = 8r2 oraz e2+f2≥ 2ef
to mamy tezę:
|AC|2+|BD|2≥16r2
♣♣♣♣♣♣♣♣♣♣♣♣♣