Analityczna z elementami analizy
Freak: | | (x−2)2 | |
Funkcja f(x)= |
| ma ekstrema dla argumentów x1 i x2. Punkty A=(x1,f(x1)), |
| | 2x | |
B=(x
2,f(x
2)) są dwoma wierzchołkami trójkąta prostokątnego ABC. Wyznacz współrzędne
wierzchołka C wiedząc, że on do osi OY. Rozważ wszystkie przypadki.
Policzyłem pochodną tej funkcji oraz jej ekstrema i wyszło mi, że A=(−2,−4) oraz B=(2,0),
natomiast nie rozumiem drugiej części zadania: "Wyznacz współrzędne wierzchołka C wiedząc, że
on do osi OY". Czy byłby ktoś w stanie mi pomóc?
14 gru 21:14
a7:
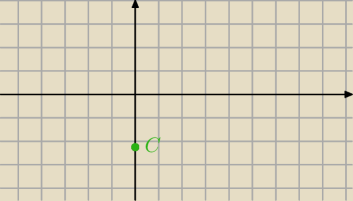
wierzchołek C leży (należy) na /do osi OY czyli ma współrzedne zero oraz y
c C=(0,y
C)
14 gru 21:17
a7:
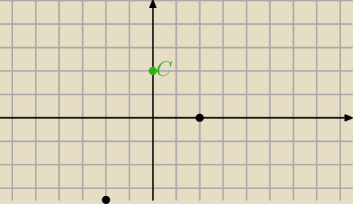
noi są chyba dwa przypadki albi lezy on powyżej osi OX
14 gru 21:25
a7:
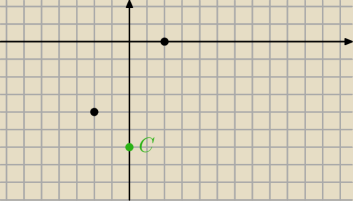
albo poniżej
14 gru 21:25
a7: wiadomo, że trójkąt ABC jest prostokątny czyli kwadraty długości przyprostokątnych można
zsumować i wyjdzie porzeciwprostokątna (jej długość), i wyliczamy C
14 gru 21:26
a7:
1) oblicz długość AB
2) długość AC i długość BC z wzoru na długoś odcinka
3) podstawiamy do Tw. Pitagorasa i powinno wyjść (?)
14 gru 21:29
a7: czy dasz już radę?
14 gru 21:29
Freak: tak, już wszystko rozumiem, o takie wytłumaczenie mi chodziło. Dziękuje bardzo

14 gru 21:30
a7: |AB|=4√2
|AC|=√4+(yc−4)2 |BC|=√4+yc2
z Tw. Pitagorasa:
1. yC>0
|AC|2=|AB|2+|BC|2
yC=2
2.yc<0
z Tw. Pitagorasa
|AC|2=|AB|2+|BC|2
yC=−6
ODP> C=(0,2) lub C=(0,−6)
(?)
14 gru 21:35
Freak: prócz tych dwóch poprawnych odpowiedzi, jest jeszcze C=(0,−2−2√2) lub C=(0,−2+2√2)
14 gru 21:38
a7: ale wyszły Ci? te dwie dodatkowe?
14 gru 21:41
a7: a tak już widzę
14 gru 21:42
a7: dla każdego z przypadków C może być poniżej lub powyżej osi OX
14 gru 21:42
Freak: wyszło mi tylko C=(0,2) i C=(0,−6)
14 gru 21:44
a7: czyli
1. 4+(yC+4)2=32+4+yC2
yC=2 lub yC=−2+2√2
podobnie
2.
14 gru 21:45
a7:
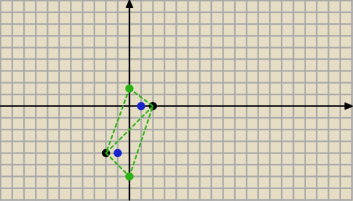
14 gru 21:46
a7: jeszcze raz
14 gru 21:47
a7: nie , nie widzę jednak, może ktoś mnie skoryguje...
14 gru 21:52
b4:
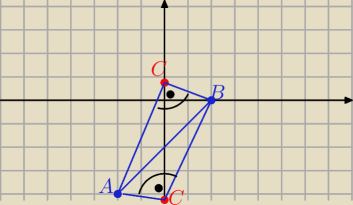
14 gru 21:55
a7: o jest i B4 z odsieczą
14 gru 21:56
b4:

14 gru 21:57
Min. Edukacji: i to ma być prostokąt?😃
14 gru 22:07
a7: AB2=AC2+BC2
32=(√4+(−4−yC)2)2+(√4+(−yC)2)2
no i teraz wychodzi
14 gru 22:07
a7: 22:07 to jest pierwszy przypadek do rysunku 21:55
14 gru 22:08
 wierzchołek C leży (należy) na /do osi OY czyli ma współrzedne zero oraz yc C=(0,yC)
wierzchołek C leży (należy) na /do osi OY czyli ma współrzedne zero oraz yc C=(0,yC)
 noi są chyba dwa przypadki albi lezy on powyżej osi OX
noi są chyba dwa przypadki albi lezy on powyżej osi OX
 albo poniżej
albo poniżej



