Przekroje. Katarzynaidruzyna: Krawędź boczna prawidłowego ostrosłupa sześciokątnego ma długość 8 dm, a krawędź podstawy 4 dm. Przez środki dwóch sąsiednich krawędzi podstawy poprowadzono płaszczyznę prostopadłą do podstawy. Oblicz pole otrzymanego przekroju. Z rysunkiem. Z góry dziękuję za pomoc.

a7:

janek191: Np. Tw. kosinusów lub z zastosowaniem funkcji cosinus dla 30^o.

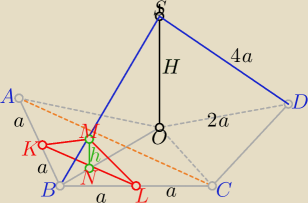
b4: Przekrój jest trójkątem równoramiennym KLM

	1
P(ΔKLM)=		|KL|*|MN|
	2

	1
|KL|=		|AC|= a√3 i |OS|=H= 2a√3
	2

	1		1
ΔBMN∼ΔBOS w skali k=		to h=		H=a√3/2
	4		4

	1		a√3
P(KLM)=		*a√3*
	2		2

	3a2
P(KLM)=
	4

============= dla 2a=4 to a=2 P(KLM)=3dm² ♣♣♣♣♣♣♣♣♣♣

Katarzynaidruzyna: Dziękuję.