Rozkład normalny Maja: Waga jabłka z pewnego sadu jest zmienną losową o rozkładzie normalnym z wartością średnią 260 g i odchyleniem standardowym 50 g. Hurtownik nabył 400 sztuk jabłek z tego sadu i chce podzielić te jabłka na trzy części: 1 część − 100 najmniejszych jabłek, 2 część − 100 największych jabłek, 3 część − 200 jabłek średniej wielkości. a) Jaką wagę graniczną powinien przyjąć hurtownik dla jabłek najmniejszych, a jaką dla największych? b) Ile sztuk jabłek mających wagę powyżej 300 g należy się spodziewać w zakupionej partii jabłek? Wiem tylko tyle, że N(260,50), trzeba wyznaczyć jakieś P(X<x) i że trzeba będzie wykonać standaryzację, ale poza tym nie bardzo sobie radzę w zadaniach tego typu. Wytłumaczyły mi ktoś ten przykład?

ABC: w b) jest mniej pisania

	X−260		4
P(X>300)=P(X−260>40)=P(		>		)
	50		5

I z tablic rozkładu normalnego znajdujesz wartość dystrybuanty dla 0,8

Maja: Okej. A co powinnam wyliczyć w a) ?

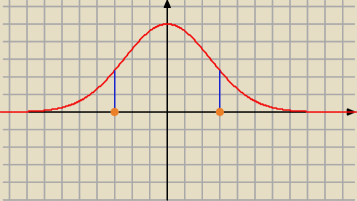
ABC: powinnaś znaleźć w tablicach standardowego rozkładu gdzie pole wynosi 0,25 a gdzie 0,75 czekaj zrobię ci rysunek , a potem to odstandaryzować żeby znaleźć te wagi

Min. Edukacji: albo policz kratki

Maja: Czyli to w środku to są te jabłka średniej wielkości, po lewej najmniejsze, a po prawej największe?

ABC: tak , środek ma pole 0,5 bo 200/400 a boki 0,25 bo 100/400

Maja: Super, dziękuję