trapez
michał:
Oblicz pole trapezu równoramiennego,którego górna podstawa
ma długość 9 , ramię ma długość 10 i przekątna ma długość17
10 gru 21:38
chichi:
Tw. Carnota załatwi sprawę

10 gru 21:46
Mila:
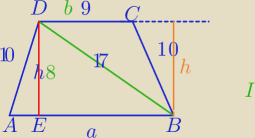
Inny sposób:
| | a+b | |
1) W trapezie równoramiennym: |EB|= |
| |
| | 2 | |
2) P
ΔDCB:
Wzór Herona wykorzystamy:
18−17=1
18−10=8
18−9=9
P
ΔDCB=
√18*1*8*9=36
3) W ΔDEB:
17
2=8
2+|EB|
2
|EB|=15
3) P
ABCD=15*8=120
10 gru 22:42
b4:
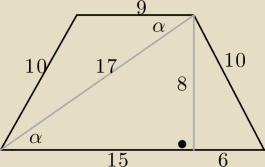
P=120
10 gru 22:44
Król Artur:
 b4
b4
11 gru 00:20
Mariusz:
Samo tw Carnota to trochę mało
Przydałoby się pokazać że suma kątów A+C=180
I zastanowić się czy chcemy liczyć długość wysokości a później pole trapezu ze wzoru
czy chcemy sumować pola tych trójkątów na które podzieliła trapez przekątna
Jeśli chcielibyśmy liczyć długość wysokości to z tw Carnota skorzystalibyśmy trzy razy
(raz będzie to przypadek szczególny zwany tw Pitagorasa)
Pomysł z tw Carnota całkiem niezły bo mają go w programie nauczania
W ΔBCD
17
2=9
2+10
2−2*10*9*cos C
289=181−180cos C
108=−180cos C
| | 3 | | 4 | |
cos C=− |
| , sin C = |
| |
| | 5 | | 5 | |
sinus obliczamy z jedynki trygonometrycznej a będzie potrzebny do wzoru na pole trójkąta
W ΔABD
17
2=10
2+a
2−2*10*a*cos(180−C)
189=a
2−12a
a
2−12a+36=225
(a−6)
2−15
2=0
(a−21)(a+9)=0
cos A = cos(180−C)=−cos(C)
| | 3 | | 4 | |
cos A = |
| , sin A = |
| |
| | 5 | | 5 | |
| | 1 | | 4 | | 1 | | 4 | |
P = |
| *9*10* |
| + |
| *21*10* |
| |
| | 2 | | 5 | | 2 | | 5 | |
P=4*(9+21)
P=4*30
P=120
11 gru 07:52
b4:
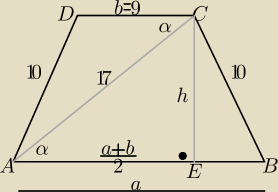
Zobacz
Mariusz 
| | 289+81−100 | | 15 | |
z tw. Carnota w ΔACD cosα= |
| = |
| |
| | 2*17*9 | | 17 | |
| | |AE| | | a+b | |
to w ΔAEC |
| =cosα ⇒|AE|=15 = |
| i |EC|=h=8 |
| | 17 | | 2 | |
P=15*8 =120
i po ptokach

11 gru 11:40
chichi:
O to chodziło @
Eta 

11 gru 11:51
PW: Jeszcze prościej = na poziomie podstawówki. Posłużę się rysunkiem z 10 grudnia, 22:44, bez
liczb, które stanowią rozwiązanie.
Przekątna i wysokość trapezu wyznaczają dwa trójkąty prostokątne. Jeden ma przeciwprostokątną
długości 17, a przyprostokątne o długościach (9 + b) i h, zaś drugi − przeciwprostokątną o
długości 10 i przyprostokątne h oraz b.
| | ⎧ | (9 + b)2 + h2 = 172 | |
| | ⎩ | b2 + h2 = 102 |
|
Wystarczy odjąć stronami i mamy b = 6, a po podstawieniu do drugiego z równań wyliczamy h = 8.
Dwa razy twierdzenie Pitagorasa i łatwy układ równań, żadnych Carnotów czy funkcji
trygonometrycznych.
11 gru 15:40
Mariusz:
No i rozwiązanie zaprezentowane przez PW jest chyba najprostsze
PW z tym że żadnych Carnotów to nie jest aż tak do końca prawda bo tw Pitagorasa to
szczególny przypadek tw Carnota
Eta tylko skąd wiemy że ∡CAB ma taką samą miarę co ∡DCA
| | a+b | |
oraz dlaczego AE ma długość |
| |
| | 2 | |
Najbardziej mi się podoba jednak rozwiązanie zaprezentowane przez PW
14 gru 21:38
b4:
α kąty naprzemianległe ! więc jakie mają miary?

14 gru 21:43
Mariusz:
Z tą długością to jednak prosty rachunek dzięki temu że mamy trapez równoramienny
a ja mało spałem
ale co z tymi miarami kątów ?
Tego nadal nie widzę
14 gru 21:45
Mariusz:
Eta ja za niecałą godzinę będę obchodził 40. urodziny
a nauczycielem nie jestem aby pamiętać takie szczegóły
14 gru 21:48
b4:
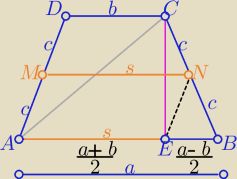
W trapezie równoramiennym :
| | a+b | | a−b | |
|AE|=s= |
| i |EB|= |
| |
| | 2 | | 2 | |
14 gru 21:50
b4:
Dużo zdrowia !

14 gru 21:52
a7:
Najlepsze życzenia!
Inspiracji i natchnienia!

14 gru 21:54
14 gru 22:38

 Inny sposób:
Inny sposób:
 P=120
P=120
 b4
b4
 Zobacz Mariusz
Zobacz Mariusz 




 W trapezie równoramiennym :
W trapezie równoramiennym :


 ! Sto lat
! Sto lat !
! 