Geo analityczna Cyz: W robię abcd którego pole jest równe 10 dane są przeciwległe wierzchołki A(1,1) B(3,5) wyznacz c i d Wyznaczyłem ze prosta dB ma wzór y=−1/2x + 4 I dalej nwm co robić chciałam ze trojkat acd i ze wzoru na pole trojkata o wierzchołkach abc ale nie wychodzi

janek191: W rombie !

janek191: Przeciwległe wierzchołki to np. A i C.

Cyz: To wiem, tylko jak już wyznaczyłem równanie prostej DB Y=−1/2x+4 to noe wiem co dalej

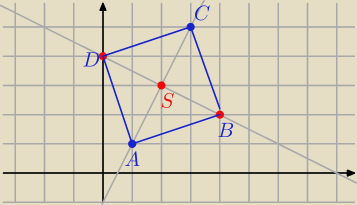
janek191: pr. AC

	5 −1
a =		= 2
	3−1

y =2 x +b i A = (1,1) więc 1 = 2*1 + b ⇒ b = −1 y = 2 x − 1 lub 2 x − y − 1 = 0 ======== =========== S = ( 2, 3) I AC I = √4 + 16 = 2√5 P = 0,5 *2√5* I BD I = IBD I *√5 = 10 I BD I = 2√5 Romb jest kwadratem. Odległość B od S jest równa √5. Prosta prostopadła do pr AC przechodząca przez S: y = −0,5 x + c 3 = −0,5*2 + c ⇒ c = 4 y = −0,5 x + 4 C = ( 4,2) D =( 0, 4)

Cyz: Skąd wychodzi ze c to 4,2 i d(0,4)

janek191: Miało być: B =( 4,2) D =(0,4) Z rysunku. Można też obliczyć B = ( x, y) = ( x, −05 x + 4) Mamy S = ( 2,3) więc I BS I² = (√5)² = 5 ( x − 2)² + ( − 0,5 x+ 1)² = 5 x² − 4 x + 4 + (0.25 x − x + 1) = 5 1,25 x² −5 x = 0 x*(1.25 x − 5) = 0 x = 0 ⇒ y = −0,5*0 + 4 = 4 D =( 0, 4) lub 1,25 x = 5 x = 4 ⇒ y = −0,5*2 + 4 = 2 B = ( 4, 2)

b4: Romb jest kwadratem to |AS| =|BS|= |CS|=|DS| i wektory AS⊥BS S(2,3) i z warunku prostopadłości wektorów → → AS=[1,2] to BS=[ −2,1] lub [2,−1] więc 2−x_B=−2 i 3−y_B= 1 ⇒ x_B=4 i y_B=2 , B=(4,2) D=(4−4, 6−2)= (0,4)

Cyz: Ok, dziękuje! już rozumiem