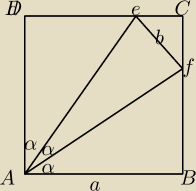
 W kwadracie ABCD punkty e i f nalezą odpowiednio do boków DC i BC oraz odcinki AE i AF dzielą
kąt BAD na trzy równe kąty. Wykaż że jeśli boki kwadratu mają długość a>0 zaś odcinek ef ma
długość b>0 to 3b2 = 4a2(2−√3)
Doszłam do tego, że można skorzystać tutaj z własności trójkątów charakterystycznych, ale cały
czas wychodzi mi 3b2 = 4a2 i nie umiem znaleźć własnego błędu, prosze o pomoc
W kwadracie ABCD punkty e i f nalezą odpowiednio do boków DC i BC oraz odcinki AE i AF dzielą
kąt BAD na trzy równe kąty. Wykaż że jeśli boki kwadratu mają długość a>0 zaś odcinek ef ma
długość b>0 to 3b2 = 4a2(2−√3)
Doszłam do tego, że można skorzystać tutaj z własności trójkątów charakterystycznych, ale cały
czas wychodzi mi 3b2 = 4a2 i nie umiem znaleźć własnego błędu, prosze o pomoc
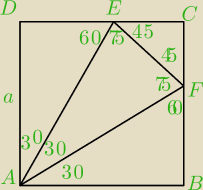
| 2a | a | |||
z trójkata ekierki AE=AF= | DE=AE/2= | |||
| √3 | √3 |
| a(√3−1 | ||
EC=a−DE=a−U{a{√3}}= | ||
| √3 |
| a(√3−1 | ||
z trókata ECF EF=EC√2= | *√2 | |
| √3 |