okrąg opisany na czworokącie
kochammatematyke123: Na czworokącie wypukłym ABCD można opisać okrąg. Przekątne AC i BD przecinają się w punkcie P
pod kątem prostym. Wiedząc, że |AP|=15 cm, |PC|=6 cm oraz |PD|=8 cm, oblicz:
(a) długości boków czworokąta ABCD,
(b) promień okręgu opisanego na tym czworokącie.
5 gru 15:44
a7:
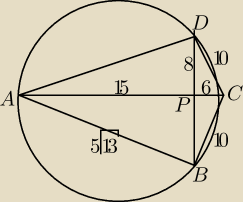
czworokąt ten to deltoid (?) (gdyż przekątne są pod kątem prostym)
z tw. Pitagorasa CD=BC=10 AB=AD=5
√13
5 gru 16:34
a7: błędnie uznałam AC za średnicę
5 gru 16:52
a7: ?
5 gru 16:52
Iryt:
|AD|=17
|DC|=10
Z tw cosinusów>
21
2=10
2+17
2−2*10*17*cosD
Stąd wniosek, że ADC nie jest kątem prostym lecz rozwartym.
Popraw obliczenia.
5 gru 17:26
a7: ale AC też nie jest średnicą tak?
5 gru 17:31
a7: aj tak
5 gru 17:31
a7: już moment
5 gru 17:32
a7:
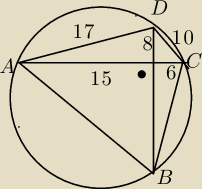
5 gru 17:36
Iryt:
8*|PB|=6*15
5 gru 17:56
Iryt:
| | 13 | |
cosD=− |
| − źle mi się napisało  |
| | 85 | |
5 gru 19:09
 czworokąt ten to deltoid (?) (gdyż przekątne są pod kątem prostym)
z tw. Pitagorasa CD=BC=10 AB=AD=5√13
czworokąt ten to deltoid (?) (gdyż przekątne są pod kątem prostym)
z tw. Pitagorasa CD=BC=10 AB=AD=5√13

