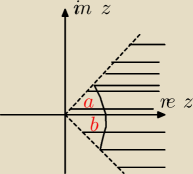
Narysuj zbiór na płaszczyźnie zespolonej DQ: Witam mam za zadanie narysowanie takiego zbioru na płaszczyźnie zespolonej:

	π		i		3π
{ z∊ℂ:		< arg(		) <		∧ re(z2) > 0}
	4		z		4

	π		π
Czy te rozwiązanie jest prawidłowe ? Kąty a i b to kolejno		,−
	4		4

PW: Tak "z pamięci" nie da się przytaknąć, więc policzę po swojemu (jeśli nieudolnie, to wybacz Szanowny Czytelniku). Dla z = u + v i, u, v ∊ R z² = u² − v² +2uv i re(z²) = u² − v² > 0 ⇔ (u − v)(u + v) > 0 ⇔ (u − v > 0 ∧ u + v > 0) ∨ (u − v < 0 ∧ u + v < 0) ⇔ (1) (v < u ∧ v > − u) ∨ (v > u ∧ v < − u)

	i		z̅ i		v + ui		v		u
		=		=		=		+		i = cosφ + i sinφ
	z		z̅z		|z|2		|z|2		|z|2

(φ jest argumentem). Jeżeli oznaczyć z = cosς + i sinς arg z = ς, to

	u		v
cosς =		, sinς =		.
	|z|2		|z|2

Widać więc, że cosφ = sinς i sinφ = cosς Nierówność

	π		3π
		< φ <
	4		4

oznacza, że

	√2		√2
−		< cosφ <
	2		2

a więc

	√2		√2
−		< sinς <
	2		2

	π		π
(2) −		< ς <
	4		4

Oba warunki (1) i (2) są spełnione dla par zaznaczonych przez Ciebie na rysunku