Rozwiązać równania macierzowe Styx: Rozwiązać równania macierzowe: | 2 −3 | | 2 3 | a) | 4 −6 | X = | 4 6 | | 2 3 | | 1 −2 | b) | 4 6 | X = | 0 4 | | 3 −1 | | 2 −1 | | 12 16 | c) | 5 −2 | X | 4 2 | = | 1 3 | | 3 −1 1 | | 3 9 7 | d) | 4 −3 3 | X = | 1 11 7 | | 1 3 0 | | 7 5 7 |

sushi: zapisz swoje obliczenia, bo nikomu nie będzie się chciało tyle liczyć

Styx: Właśnie nwm za bardo jak. W pierwszym wyznaczniki obu macierzy są 0 więc chyba nie moge pomnożyć przez macierz odwrotną, a jeśli tak to nie wiem jak inaczej to zrobić. W 2 wydaje mi się, że w ogóle jest to sprzeczne.

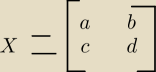
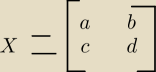sushi: a jakbyśmy policzymy z macierzy 2a−3c=2 2b−3d=3 4a−6c=4 4b−6d=6 i widzimy, że 1 i 2 równianie to jest 2 x odpowiednio 3 i 4 więc zostanie: 2a−3c=2 −−> 2a= 2+3c −−> a = 1 +1,5c 2b−3d=3 −−> 2b= 3+3d −−> b = 1,5 +1,5d