Wyznacz równanie okręgu wpisanego w trójkąt, Klaudia: Wyznacz równanie okręgu wpisanego w trójkąt, którego boki są zawarte w osiach układu współrzędnych i w prostej 3x + 4y − 24 = 0

wredulus_pospolitus: i problem polega na Trójkąt ten będzie trójkątem prostokątnym, gdzie kąt prosty jest przy wierzchołku w (0,0). 0) wyznaczamy punkty przecięcia prostej z osiami 1) Wyznaczamy długość przeciwprostokątnej oraz przyprostokątnych (oraz pole trójkąta)

	2P
2) Korzystając ze wzoru r =		wyznaczamy promień okręgu wpisanego
	a+b+c

3) Środek okręgu będzie miał współrzędne (r,r) 4) Zapisujesz równanie tegoż okręgu. Kooooniec

chichi:

	a+b−c
r =		jeśli Δ jest prostokątny
	2

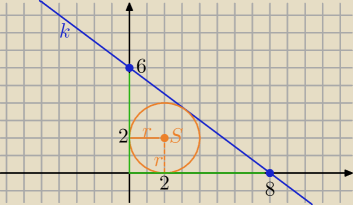
Jola: k: 3x+4y−24=0 o: (x−2)²+(y−2)²=4 ♣♣♣♣♣♣♣♣♣♣♣♣♣

Mila: 3x + 4y − 24 = 0 1) Punkty przecięcia osi układu współrzędnych: y=0 wtedy: 3x=24⇔x=8 x=0 wtedy : 4y=24⇔y=6 2)

	6+8+10
PΔ=24=		*r
	2

r=2 3) współrzędne środka okręgu: środek okręgu leży na przecięciu dwusiecznych kątów Δ; Dwusieczna kąta prostego: y=x Promień jest prostopadły do boków Δ w punktach styczności: S=(2,2) 4) równanie okręgu napisz sama

PW: Wersja z minimalnymi rachunkami, wymaga znajomości wzoru na odległość punktu od prostej. Niech S będzie środkiem okręgu wpisanego. S = (r, r) jest poprawnym oznaczeniem, gdyż S należy do dwusiecznej pierwszej ćwiartki układu współrzędnych (ma więc jednakowe współrzędne). Odległość od S do prostej 3x + 4y − 24 = 0 jest równa r (okrąg jest styczny do prostej).

	|3r + 4r − 24|
		= r, r > 0
	√32 + 42

	|7r − 24|
		= r
	√25

|7r − 24| = 5r 7r − 24 = 5r lub −(7r − 24) = 5r r = 12 lub r = 2 Sprawdzamy położenie punktu S względem prostej: dla r = 12 jest 3^.12 + 4^.12 − 24 > 0 − S leży powyżej prostej dla r = 2 jest 2^.2 = 4^.2 − 24 < 0 − S leży poniżej prostej zgodnie z warunkami zadania Odp. S = (2, 2) i r = 2, zatem równanie okręgu wpisanego ma postać (x − 2)² + (y − 2)² = 2².