Oblicz pole powierzchni całkowitej i objętość ostrosłupa. Monika: W ostrosłupie prawidłowym trójkątnym krawędź podstawy ma długość 12 cm .Kąt nachylenia ściany bocznej do płaszczyzny podstawy ma miarę 60 stopni.Oblicz pole powierzchni całkowitej i objętość ostrosłupa.

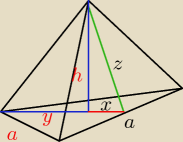
Łukasz: Podstawą jest trójkąt równoboczny o boku a=12 cm. H− wysokość podstawy na rysunku H=x+y

	a√3
H=
	2

	1		1		a√3		a√3		12√3
x=		H, z tego x=		*		=		=		=2√3 cm
	3		3		2		6		6

	2
y=		H,
	3

z=2x=2*2√3=4√3cm h=x√3=2√3*√3=6 cm Obliczam objętość

	1		1		a2*√3		1		122*√3
V=		Pp*h=		*		*h=		*		*6=72√3 cm3
	3		3		4		3		4

Pole powierzchni składa się z podstawy − trójkąt równoboczny i 3 trójkątów o podstawie a i wysokości z.

	a2*√3		az		122*√3		12*4√3
Pc=Pp+Pb=		+3*		=		+3*		=
	4		2		4		2

	144*√3		144√3
=		+		=36√3+72√3=108√3 cm2
	4		2

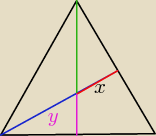
Łukasz: W trójkącie równobocznym punkt przecięcia wysokości dzieli tą wysokość na odcinki równe 2/3h i 1/3h. Na tym rysunku odcinki niebieski i zielony wynoszą 2/3h , a czerwony i fioletowy 1/3h.

fgfds: Δ∞∞≥δδβ⇒⇔≠⇔∫≥≥≤∞ΔΩ⊂→⇒

daria: długość krawędzi podstawy ostrosłupa prawidłowego trójkątnego wynosi 30 stopni. kat nachylenia ściany bocznej do płaszczyzny podstawy ma miarę 60 stopni. oblicz V i Pc

daria: W ostrosłupie prawidłowym sześciokątnym, krawędź podstawy ma długość a, a kąt między ścianą boczną i płaszczyzną podstawy ma miarę α. Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa.