zadanie pdw m4rrios: Zbadaj przebieg monotoniczności, narysuj wykres f(x)= x*e^−x

Modus: f(x) = xe^−x 1. Dziedzina: x ∊ R 2. Miejsca zerowe: f(x) = 0 ⇔ xe^−x = 0 ⇒ x=0 3. Przecięcie z osią OY: f(0) = 0 ⇒ P=(0,0) 4. Granice i asymptoty: Brak asymptot pionowych.

	x
limx→∞ f(x) = limx→∞ xe−x = limx→∞
	ex

Z reguły de l'Hospitala:

	x		1
limx→∞		= limx→∞		= 0
	ex		ex

lim_x→−∞ f(x) = lim_x→−∞ xe^−x = ∞ Asymptota pozioma prawostronna y=0 (w ∞). 5. Przedziały monotoniczności: f'(x) = e^−x−xe^−x = e^−x(1−x) f ↗ ⇔ f'(x) > 0 ⇔ e^−x(1−x) > 0 ⇔ 1−x > 0 ⇔ x < 1 f ↘ ⇔ f'(x) < 0 ⇔ e^−x(1−x) < 0 ⇔ 1−x > 0 ⇔ x > 1 Funkcja jest rosnąca w przedziale (−∞, 1), a malejąca w przedziale (1,∞). 6. Ekstrema: Na podstawie powyższego: Funkcja osiąga ekstremum będące maksimum globalnym dla x = 1 równe:

	1
f(1) =
	e

7. Przedziały wklęsłości i wypukłości: f''(x) = −e^−x(1−x)−e^−x = e^−x(x−2) f''(x) > 0 ⇔ e^−x(x−2) > 0 ⇔ x−2 > 0 ⇔ x > 2 f''(x) < 0 ⇔ e^−x(x−2) < 0 ⇔ x−2 < 0 ⇔ x < 2 Funkcja jest wypukła w przedziale (2, ∞) oraz wklęsła w przedziale (−∞,2). 8. Punkty przegięcia: Na podstawie powyższego: Odcięta punktu przegięcia wykresu funkcji wynosi x = 2. Wartość w punkcie przegięcia:

	2
f(2) =
	e2

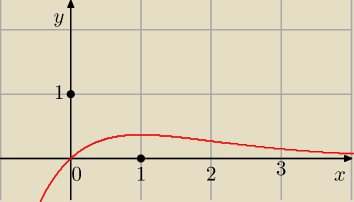
9. Wykres funkcji (ew. tabela, którą sobie podaruje, wykres możesz narysować w Geogebra/desmos). 10. Zbiór wartości:

	1
Wf = (−∞,		>
	e

Można sprawdzić, bo nie chce mi się czytać moich bzdur.

janek191: