pomoc w zadaniach Oliwier: Dzień dobry zakładam ten temat w którym będę dodawał zadania które sprawiają mi problem. Pozdrawiam

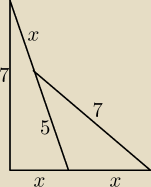
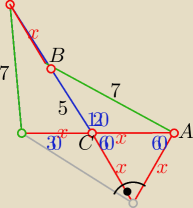
Oliwier: Wyznacz długość x.

Oliwier: Wyznacz te wartości parametru m, dla których równanie (m−mx−x²)(m²+|3x+2|−5)=0 ma tylko jeden pierwiastek.

janek191: x = 2,4

chichi: Nie zgodzę się z przedmówcą

Kacper: Ten rysunek kiepski, czy trójkąt jest prostokątny? Po co nam zatem ten trójkąt 5, 7, x?

chichi: Sam sobie odpowiadasz, traktujmy zadania takie jakie są, a nie przypuszczajmy. Czy na rysunku jest kąt prosty? Nie ma, więc nie domniemujmy, że może tam jest, bo rysunek sugeruje. Rozwiązywalibyśmy w ten sposób różne zadania, ale faktem jest, że gdyby rysunek był dokładniejszy, to nie byłoby takich niepewności..

Oliwier: Przepraszam państwa tak mi się narysowało ale na rysunku który mam widać że tam jest więcej niż 90stopni czy ktoś wie jak rozwiązać te zadania?

kerajs: Zadanie z geometrii rozwiążesz porównując kosinusy kątów przy wierzchołku z którego wychodzą dwa odcinki x. Odpowiedź na drugie zadanie zależy od tego co rozumiesz przez pierwiastek. ( dla mnie odpowiedź to m=−√5)

chichi: @kerajs (1) dłuuuugo, można sprtynie, nie chce mnie się rysować teraz, może później, a może przyjdzie któraś z Pań od geometrii i wrzuci rozwiązanie (2) dla mnie m ∊ {−4, −√5}

kerajs: Ad 1 Możliwe. Zobaczyłem zadania i od razu odpisałem, nie bawiąc się w obliczenia. Ad 2 Właśnie o to chodziło gdy pisałem: ''Odpowiedź na drugie zadanie zależy od tego co rozumiesz przez pierwiastek''. Dla mnie dla m=−4 to równanie ma dwa równe pierwiastki ( i ogólnie równanie kwadratowe ma dwa pierwiastki rzeczywiste (w tym i równe) lub żadnego). Dla innych przy m=−4 jest pierwiastek podwójny, a jeszcze inni będą twierdzić że równanie ma tylko rozwiązania, a nie jakieś pierwiastki.

kerajs: Ad 1 Postawię na x=3

chichi: No to jutro stawiaj w totka

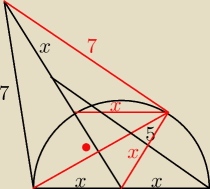
kerajs: Obstawiam, gdyż nie jestem pewien rachunków, a nie dlatego że zgaduję. Inne podejście niż zaproponowane wyżej: Dorysowuję drugi trójkąt o bokach x,7, 5+x (tak że wierzchołek z którego wychodzą dwa odcinki x jest ich punktem symertii) i dzielę go odcinkiem x tak że dostaję trójkąt równoboczny o boku x i lustrzany trójkąt o bokach x,5,7. Teraz szukany x mogę wyliczyć a) z twierdzenia kosinusów skoro kąt między ramionami x i 5+x to 60 stopni b) z trójkąta prostokątnego

	x		x√3
72=(5+		)2+(		)2
	2		2

chichi: A skąd mnie to wiedzieć dlaczego Ty stawiasz?

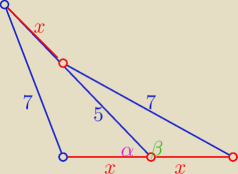
Eta: cosβ= −cosα z tw. cosinusów

	x2+(x+5)2−49		−x2−25+49
cosα=		i cosβ=−cosα to cosα=
	2x(x+5)		10x

porównując i upraszczając przez x>0 otrzymujemy równanie ................................. x³+15x²+26x−240=0 (x−3)(x²+18x+80)−0 x=3 ♦♦♦♦

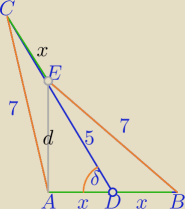
Mila: 1) ΔAED: d²+7²=2*(5²+x*x) d²=2x²+1 2) ΔADE: tw. cosinusów:

	24−x2
cosδ=
	10x

3) ΔADC: tw. cosinusów

	24−x2
49=x2+(x+5)2−2x(x+5)*
	10x

Otrzymujemy równanie : x³+15x²+26x−240=0 x=3

chichi: Kąciki podpisać etc. i mamy x = 3, nie chce mi się już walczyć z tym edytorem o tej godzinie

Mila:

Eta: z tw. cosinusów wΔABC 49=x²+25+5x ⇒ x²+5x−24=0 ⇒ (x−3)(x+8)=0 x=3 ♥♥♥♥

an: 7²=x²+(x+5)²−2x(x+5)cos60^o x²+5x−24=0 x=3