pole mumin: Dany jest trójkąt o bokach długości 5√2, √10, 2√13 Oblicz pole tego trójkata

kerajs: Postawię na: P=11 .

ABC: problem polega na? możesz ze wzoru Herona , a jak za trudne rachunki to tw cosinusów − cosinus , z niego sinus i wzór sinusowy

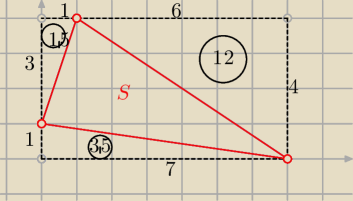
Eta: S=28−(1,5+3,5+12) S=11 ♦♦♦♦♦

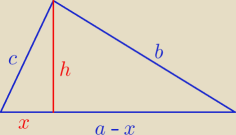
janek191: a = 2√13 b = 5√2 c = √10 Mamy ( 2√13 − x)² + h² = 25*2 x² + h² = 10 więc ( 52 − 4√13 x + x²) − x² = 40 12 = 4√13 x

	3
x =
	√13

	9		121
h2 = 10 −		=
	13		13

	11
h =
	√13

P = 0,5 a*h = 11 j² ================

PW: Brawo Eta − kolejny raz pokazuje genialnie prosty wzór, którego uczyli w gimnazjum. Kto wie, jaką nazwę ma ten wzór?

ABC: Rozwiązanie Ety jest z cyklu " jak ja mam na to wpaść? " jest piękne jeśli już się je zna

chichi: @PW ale, że niby jaki wzór? Sposób zaproponowany przez @Eta to dobrze znany myk, ale nie zawsze jest tak ładnie i prosto tak, jak w tym przypadku

kerajs: ''ABC: Rozwiązanie Ety jest z cyklu " jak ja mam na to wpaść? " jest piękne jeśli już się je zna'' Czyżbyś sugerował że mumin to także Eta? ''chichi: (...) ale nie zawsze jest tak ładnie i prosto tak, jak w tym przypadku'' Sądzę, że nawet ten ''prosty'' przykład jest bardziej czasochłonny niż rachunki ABC czy janek191, gdyż rozkład liczby na sumę dwóch kwadratów wcale nie jest oczywistym. PS Mimo wszystko doceniam elegancję ''rozwiązania'' Ety.

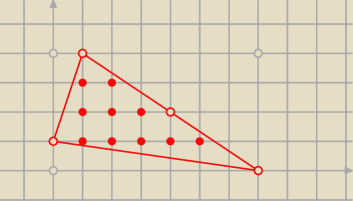
Eta: Wzor Picka

	B
S=W+		−1
	2

W − ilość punktów kratowych wewnątrz trójkąta B − ilość punktów kratowych na brzegu trójkąta

	4
S= 10+		−1
	2

S=11 ♥♥♥♥ Pozdrawiam kolegę PW

chichi: No dobrze, ale Ty na pewno nie korzystałaś ze wzoru Picka tylko pól trójkątów prostokątnych... Co wynika z samego obrazka..

kerajs: Clou powyższych rozwiązań to: ''jak stwierdzić że wierzchołki tego trójkąta są punktami kratowymi?'', bo stąd dopiero uzyskuje się obrazek, a dopiero z niego wynik.