Graniastosłupy prawidłowe Joanna: Krawędź boczna graniastosłupa prawidłowego trójkątnego jest dwa razy dłuższa od krawędzi podstawy. Oblicz sinus kąta nachylenia przekątnej ściany bocznej do płaszczyzny zawierającej sąsiednią ścianę boczną. Proszę bardzo o pomoc.

a ja nie wiem: a²+(2a)²=x² − x to przekatna sciany bocznej x = √5*a z twierdzenia cosinusow obliczamy cos kata niebieskiego a² = (√5*a)² + (√5*a)² − 2*(√5*a)*(√5*a)²* cosα /:a² 1 = 5 + 5 − (2 * 5 * cosα) cosα = 9/10 z jedynki trygonometrycznej i wiemy ze kat niebieski bedzie nalezal do przedzialu α∊(0,90) wiec nie martwimy sie czescia ujemna bo cosinus i sinus sa dodatnie w tym przedziale (sinα)² = 1 − (cosα)² (sinα)² = 1 − 81/100 sinα = √19/10 lub sinα = −√19/10 wybieramy pierwsze rozwiazanie i koniec Odp. sinα = √19/10

a ja nie wiem: blad przy kopiowaniu a² = (√5*a)² + (√5*a)² − 2*(√5*a)*(√5*a)*cosα

Eta:

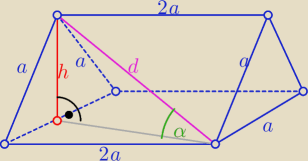
	a√3
h=		i d=√a2+(2a)2= a√5
	2

	h
sinα=
	d

	√15
sinα=
	10

♣♣♣♣♣♣♣♣♣♣ i po ptokach

Eta: A ja wiem,że Ty " a ja nie wiem" bajki piszesz

Joanna: Dziękuję bardzo za pomoc.

janek191: Dobrze, że Eta wróciła Prosto i na temat.