Funkcja kwadratowa - max i min wartości w przedziale
Rodiel: Wyznacz wzór funkcji kwadratowej f w postaci ogólnej, wiedząc, że jej wykres jest symetryczny
względem prostej x−4=0, jednym z jej miejsc zerowych jest liczba 6, a najmniejsza wartość
funkcji f w przedziale <1,3> jest równa −2.
15 lis 14:06
Rodiel: Na razie ustaliłam, że p=4 (oś symetrii to x=4) i drugie miejsce zerowe to 2 (bo
(x1+x2)/2=p). Stąd mam wzór w postaci iloczynowej f(x)=a(x−6)(x−2). Nie mogę wypatrzeć
monotoniczności i nie wiem czy f(1)=−2 czy to f(3)=−2. Zasadniczy problem widzę w tym, że
przedział <x1, x2> przecina się z przedziałem z polecenia i p nie należy do przedziału z
polecenia.
15 lis 14:10
ICSP: Musisz rozpatrzeć dwa przypadki.
Jeden gdy
f(1) = −2
oraz drugi gdy
f(3) = −2
15 lis 14:47
Rodiel: Też o tym pomyślałam, ale podręcznik podaje tylko jedno rozwiązanie z a<0.
15 lis 14:50
Rodiel: Rozważałam błąd w podręczniku lub jakąś sprzeczność w jednym z tych przypadków, ale nie mogę
żadnej znaleźć.
15 lis 14:55
chichi:
No i jaki jest problem weryfikacją błędu? Sprawdź czy ten drugi przypadek, który Ci wyszedł
jest niesprzeczny z warunkami z polecenia, jeśli tak należy go uznać koniec kropka

15 lis 14:58
Rodiel: Możliwe, niemniej rozważam też sytuację, że pojawia się nieoczywista sprzeczność, której nie
dostrzegam. Właśnie dla tej sprzeczności tu przyszłam

15 lis 15:24
ICSP: zobacz czy przedział [1,3] nie jest z jednej strony otwarty.
15 lis 15:25
Rodiel: Nie jest.
15 lis 16:15
chichi:
Dobra napisz jakie wyszły Tobie dwa przypadki, a ja sprawdzę niesprzeczność

15 lis 16:29
Rodiel: f(x)=−2/5(x−6)(x−2)=−2/5x2+16/5x−24/5
oraz
f(x)=2/3(x−6)(x−2)=2/3x2−16/3x+8
15 lis 17:08
Rodiel: a=−2/5 wychodzi z zał.: f(1)=−2, czyli parabola "smutna", a a=2/3 z zał.: f(3)=−2, czyli
parabola "uśmiechnięta".
15 lis 17:18
chichi:
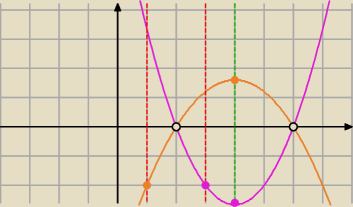
15 lis 17:33
Rodiel: Też sprawdzałam graficznie. Czy mogę wnioskować, że również nie widzicie tej sprzeczności i
twórcy podręcznika przeoczyli brak w poleceniu danych pozwalających na ustalenie
monotoniczności tej funkcji?
15 lis 18:54
chichi:
Czy to Ty @
Karolina?

15 lis 19:10
ABC: Wyobraź sobie że twórcy podręczników też popełniają błędy czasami, a niektórzy nawet dość
często i powstają książki legendy , przez grzeczność nie podam przykładów

15 lis 19:16
chichi:
Zobacz ile czasu zaoszczędzisz nie zaglądając do tych proponowanych odpowiedzi

15 lis 19:25
Rodiel: @chichi owszem Karolina, ale nie wiem, czy ta, o której myślisz

@ABC zdaję sobie z tego
sprawę, ale raz na jakiś czas popełniam drobne byki i dzięki odpowiedziom mogę je skorygować.
Dziękuję wszystkim zaangażowanym w pomoc

Miłego wieczoru

15 lis 19:51
chichi:
My już wiemy, która

15 lis 19:55
Rodiel: To, proszę, zdradź mi tę tajemnicę

15 lis 20:00
chichi:
No ta Karolina, która o dziwo w podręcznikach, z których korzysta są same błędy w odpowiedziach
i zawala forum swoimi uwagami, nie potrafi odpowiedzieć na proste pytania, ma nerwicę natręctw
matematyczną, aspiruje na nauczycielkę etc.

jeśli to jakaś inna, to najwidoczniej Karoliny
tak mają

15 lis 20:04
Min. Edukacji: 6 godzin mielić jedno zadanie!?
15 lis 20:05
chichi:
Bo BŁONT w podręczniku, a rozwiązujący nawet nie potrafi określić poprawności swojego
rozwiązania, kabarety się tu dzieją na tym forum oststnio, jakby ktoś tych ludzi tu nasyłał

15 lis 20:08
Rodiel: To chyba jednak nie ta Karolina, bo nie pamiętam, żebym się tu wcześniej udzielała. Co do
maltretowania zadania, robiłam je jakieś 7 minut, ale chciałam mieć pewność bezbłędności. Nie
jestem nieomylna, więc poszukałam u Was pomocy, za którą jestem wdzięczna

15 lis 21:06







 @ABC zdaję sobie z tego
sprawę, ale raz na jakiś czas popełniam drobne byki i dzięki odpowiedziom mogę je skorygować.
Dziękuję wszystkim zaangażowanym w pomoc
@ABC zdaję sobie z tego
sprawę, ale raz na jakiś czas popełniam drobne byki i dzięki odpowiedziom mogę je skorygować.
Dziękuję wszystkim zaangażowanym w pomoc  Miłego wieczoru
Miłego wieczoru 


 jeśli to jakaś inna, to najwidoczniej Karoliny
tak mają
jeśli to jakaś inna, to najwidoczniej Karoliny
tak mają 

