Nierownosc Muran: Mam pytanie takie nietypowe. Czy mozna prawdziwosc takiej nierownosci dla odpowiednich a, b i c dowodzic inaczej niz z nierownosci miedzy srednimi i od razu mowie zeby nie wstawiac tego rozwiazania bo sam zrobiłem to tą metodą ale tak siedzę i myślę jakby można to ugryźć w inny sposób jakby zapominając o nierównościach między srednimi. √a²+b²+√b²+c²+√a²+c²≥(a+b+c)√2

ICSP: Dowód za pomocą nierówności między średnimi zazwyczaj jest typem dowodu wprost. Poza dowodami wprost mamy dowody za pomocą przekształceń równoważnych oraz dowody typu nie wprost. Tak więc można to zrobić inaczej, tylko po co?

Muran: Bo lubie robic dowod na kilka sposobow lubie matme i mnie to ciekawi wiec twoje pytanie po co jest zbedne. Bardziej chodzilo mi oto zeby ktos pokazal jak zrobic wlasnie inaczej a nie tylko odpowiedział tak czy nie bo to że się da wiedziałem e. Sory nie doprecyzowałem

wredulus_pospolitus: podnoś obie strony do ² ... aż w końcu (może) Ci coś wyjdzie

Muran: A moglbys spróbować bo ja podnosiłem i dostaje takie tasiemce i nie potrafie nic z nich zrobic innego

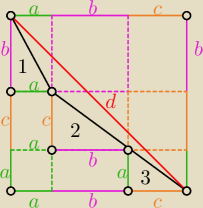
chichi: Propozycje przedmówców są nieco karkołomne, więc ja odwołam się do najpiękniejszej dziedziny matematyki jaką jest geometria (ale to tylko moje zdanie). Rozpatrzmy kwadrat o boku długości 'a+b+c'. − d = √2(a+b+c) − długości przeciwprostokątnych z trójkątów (1, 2, 3) są równe odpowiednio (√a²+b², √b²+c², √a²+c²) Z tego trójkąta zbudowanego z dwóch czarnych odcinków i jednego czerwonego mamy, że: √a²+b² + √b²+c² + √a²+c² ≥ d = √2(a+b+c) Przy czym równość zachodzi dla a=b=c (przypadek zdegenerowany, zamiast trójkąta jest odcinek) Proszę pytać w razie jakichś niejasności, a póki co stawiam ten magiczny 'kwadracik' □

Muran: Cos takiego wlasnie mialem na mysli ale nie tak trudnego. jutro sprobuje jeszcze tym sposobem podnoszenia stronami do kwadratu bo rano do szkoly. dzieki. Dam znac jutro czy cos wyszlo