równoległobok Julek: Niech ABCD będzie równoległobokiem. Punkty E, F leżą odpowiednio po bokach AB, CD tak, że ∠EDC = ∠F BC i ∠ECD = ∠F AD. Wykazać, że AB ≥ 2 · BC.

chichi: @Julek zaglądasz tu jeszcze?

Julek: Tak

chichi: Udało się coś wykombinować? Bo widzę, że brak zainteresowania na forum tym zadaniem

Julek: nie mam rozwiazania

chichi: Wrzucę zatem rozwiązanie, ale późnym wieczorem jak będę w domu

Julek: i jak?

chichi: Wyleciało mi z głowy, aktualnie jestem na uczelni, więc upomnij się jeszcze raz po południu

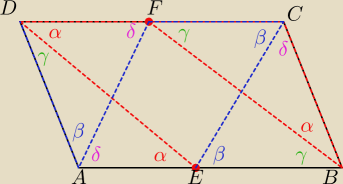
wredulus_pospolitus: ΔAED podobny do ΔCFB (podobieństwo kkk) ΔADF podobny do ΔEBC (podobieństwo kkk) stąd:

|AE|		|BC|
	=
|AD|		|FC|

|DF|		|BC|
	=
|AD|		|BE|

czyli: |AE|*|FC| = |DF|*|BE| ; podstawmy: |AE| = x ; |DF| = y ; |AE| + |BE| = 1 = |FC| + |DF| x*(1−y) = y*(1−x) −−−> x − yx = y − yx −−−> x = y −−−> |AE| = |DF| oznaczmy dodatkowo: |AD| = |BC| = a

x		a
	=		−−−> a2 = x(1−x) −−−> 0 < a2 ≤ 0.25 −−−> a ≤ 0.5
a		1−x

	|AD|		|AD|		0.5
stąd;		=		≤		= 0,5 −−−> 2|AD| ≤ |AB|
	|AB|		|AE| + |EB|		1

c.n.w.

chichi: No i tak to powinno wyglądać u mnie końcówka była:

	|AB|+|BE|		|AB|2
|CB|2 = |AB|*|BE| ≤ (		)2 =
	2		4

	|AB|
⇒ |CB| ≤
	2

⇒2|CB| ≤ |AB|

chichi: I nie przyjmowałem konkretnej długości boku

wredulus_pospolitus: ja sobie przyjąłem '1' bo chciałem zmniejszyć ilość pisania długości boku