| 3 | 4 | ||
= | |||
| 2x−m | mx−8 |
 1)
2x≠m i mx≠8
1)
2x≠m i mx≠8
| m | 8 | |||
x≠ | i x≠ | dla m≠0 | ||
| 2 | m |
| 3 | 4 | ||
= | stąd | ||
| 2x | −8 |
| 8 | ||
3m−8=0 ⇔m= | ||
| 3 |
| 32 | ||
mamy: 0*x=24− | sprzeczność− rozwiązań brak | |
| 3 |
| 8 | ||
m≠ | ||
| 3 |
| 24−4m | ||
x= | i x<0⇔ | |
| 3m−8 |
| 24−4m | 24−4m | m | 24−4m | 8 | |||||
<0 i | ≠ | i | ≠ | ||||||
| 3m−8 | 3m−8 | 2 | 3m−8 | m |
| 8 | ||
(* ) m< | lub m>6 | |
| 3 |
| 24−4m | m | ||
≠ | |||
| 3m−8 | 2 |
| 8 | ||
m=−4< | to wyłączmy ze zbioru | |
| 3 |
| 24−4m | 8 | ||
≠ | |||
| 3m−8 | m |
| 8 | ||
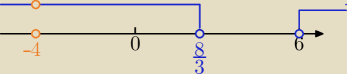
m∊(−∞,−4)∪(−4, | )∪(6,∞) | |
| 3 |