stożek Bongo: Kąt przy wierzchołku osiowego przekroju stożka jest równy 2α zaś suma wysokości i tworzącej jest równa a, znajdź objętość i pole powierzchni całkowitej stożka. Ciężka sprawa... głowię się nad tym cały wieczór... nie cierpię zadań, w których nie ma danych liczbowych..

Sabin: Czy masz do tego wyniki? Bo dziwne liczby mi wychodzą...

Bongo: niestety nie... to jest z jakiejś książki z lat 70−tych... a mógłbyś mi pokazać do czego doszedłeś? może to by jakoś rozjaśniło mój tok rozumowania

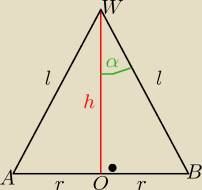
Eta: h+l = a

	h
		= cosα ..... to h= l*cosα
	l

	a
l*cosα+l= a => l( 1+cosα)=a => l=
	1+cosα

to h= Uacosα}{1+cosα}

	r		a*sinα
sinα=		=> r= l*sinα => r=
	l		1+cosα

teraz podstaw dane do wzorów

	1
V=		πr2*h =.......
	3

P_c= πr( l+r)=.......

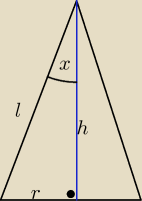
Sabin: Zamiast alfy bede pisal x dla wygody. Wysokosc jest jednoczesnie dwusieczna kata przy wierzcholku. Mamy, ze cosx = ^h_l skad h = lcosx Wiemy tez, ze h + l = a, czyli h = a − l Stad a − l = lcosx => a = l(cosx+1) => l = ^a_cosx+1 wracamy do h: h = cosx*^a_cosx+1 = ^acosx_cosx+1 Policzymy r: sinx = ^r_l => r = lsinx = ^asinx_cosx+1 Teraz wystarczy podstawic do wzorow na pole i objetosc...

Eta:

Sabin: O, teraz już mam 100% potwierdzenie. Ty rowniez

Bongo: dzięki wielkie^^ sam bym do tego wieki dochodził... this website is the best all over the world