trójkat mi19: Niech R bedzie promieniem opisanym na trójkacie ABC o bokach a, b, c. Wyznacz miary kątów tego

	a√bc
trójkąta wiedząc że R=
	b+c

janek191: Promieniem opisanym?

mi19: promieniem okręgu opisanego

mi19:

Mila: Skąd masz to zadanie?

mi19: Ze szkoły

Mila: Ze zbioru, czy z podręcznika, czy nauczyciel podał?

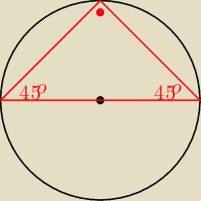
an: Czy to jedyne rozwiązanie

mi19: Nie wiem, nie mam odpowiedzi

an: Tak to jest jedyne rozwiązanie. Przeanalizuj to

	a		a*2√bc
2R=		⇒ 2R=
	sinα		(b+c)

	b
robimy podstawienie x=
	c

co jest naszym sinα rozwiązujemy nierówność sinα≤1 Trójkąt wpisany w koło nie może mieć żadnego boku większego od średnicy mamy drugą nierówność a≤2R Rozwiązanie pierwszej α=90^o Drugiej b=c czyli pozostałe kąty 45^o

Mila: 1)

a
	=2R
sinα

2a√bc		a
	=
b+c		sinα

1		2a√bc
	=
sinα		b+c

	b+c
sinα=
	2√bc

2) 0<sinα≤1⇔

	b+c
0<		≤1⇔b+c≤2√bc
	2√bc

b−2√bc+c≤0 (√b−√c)²≤0 ⇔ √b=√c⇔ b=c i sinα=1 α=90^o, b=c, a=2R β=γ=45^o =======