szesciokat wiki: Wenątrz szeciokata ABCDEF wybrano punkt P tak że AP=a, PC=b oraz ∡APC=∡AFD. Oblicz jaka może być najmniejsza możliwa długość odcinka EF.

wredulus_pospolitus: Chwileczkę ... więc de facto działamy w ten sposób: 1) Wyznaczamy punkty A, C i P w ten sposób aby |AP| = a , |CP| = b , sin(∡APC) = c 2) Konstruujemy sześciokąt ABCDEF w taki sposób, aby P leżała wewnątrz tego sześciokąta, a dodatkowo ∡AFD = ∡APC Pytanie: Konstruując sześciokąt ABCDEF jaka jest najmniejsza możliwa długość odcinka EF? Jeżeli tak to wygląda to ... moim zdaniem nieskończenie mała (zbiegająca do 0) ... innymi słowy − możemy zbudować pięciokąt ABCDF spełniający te warunki zadania

wiki: A sory to miałbyć sześciokat foremny: Wenątrz szeciokata foremnego ABCDEF wybrano punkt P tak że AP=a, PC=b oraz ∡APC=∡AFD. Oblicz jaka może być najmniejsza możliwa długość odcinka EF.

an: Zrób rysunek i zastanów się jaki może być kąt α, dalej Pitagoras

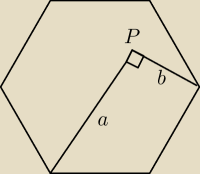
wiki: Ale nie wiem jak to rozwiązać, może coś z nierówności trójkata?

an: AC=? następnie AB, ale o co chodzi z tą najmniejszą długością, dobrze przepisałeś treść

wiki: A czemu ten kąt ma być prosty

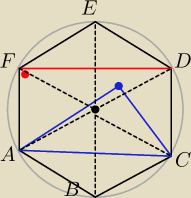
an: Jeżeli nie wiesz to policz wartość kąta AFD