Rozwiąż nierówność Zzz: (x−1)√x+4 < 2−4x

chichi: Zzzz... Śpiący jesteś? Na czym utknąłeś kochany?

Zzz: Raczej nie mam pomysłu na nick. Zrobiłem tylko założenie i nie mam pojęcia jak się za to zabrać. No bo podniesienie do kwadratu obustronnie raczej nie wchodzi w grę bo nie mamy pewności co do znaku po obu stronach ?

chichi: Podstawienie: u² = x+4 ⇒ x = u²−4, wówczas nasza nierówność przyjmuje postać: (u²−5)|u| < 2−4(u²−4) (1^o) {u ≥ 0 ∧ (u²−5)|u| < 2−4(u²−4)} ⇒ (u²−5)u < 2−4(u²−4) (2^o) {u < 0 ∧ (u²−5)|u| < 2−4(u²−4)} ⇒ (u²−5)(−u) < 2−4(u²−4) No i teraz wystarczy w tym 'podłubać'

Zzz: Teraz wszystko jasne bardzo sprytny parametr nie wpadłbym na to dzięki wielkie

chichi: Bywaj zdrów! Nie zapomnij powrócić do 'x' z 'u'

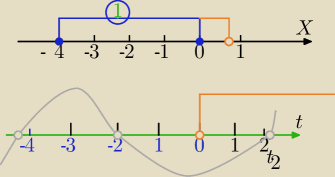
Mila: x≥−4 i (x−1)√x+4<2−4x⇔ x√x+4+4x<2+√x+4⇔ x*(√x+4+4)<2+√x+4 1) x∊<−4,0> ⇔L<P 2) x>0 √x+4=t>0 x+4=t², x=t²−4 (t²−4)*(t+4)<t+2 (t−2)*(t+2)*(t+4)−(t+2)<0⇔(t+2)*[t²+2t−9]<0 (t+2)*(t−(−1+√10))*(t−(−1−√10))<0 i t>0 t₁≈−4,2, t₂≈2,2⇔ 0<t<−1+√10⇔ √x+4>0 i √x+4<−1+√10 x+4>0 i x+4<1−2√10+10 x>−4 i x<7−2√10 x∊<−4,7−2√10)