Wykaż, że dla relacji zwrotnej R, równość R ◦ R = R jest równoważna „przechodnoś xMOROx: Wykaż, że dla relacji zwrotnej R, równość R ◦ R = R jest równoważna „przechodności” relacji R.

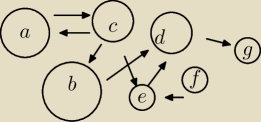
Maciess: Rozpisałeś z definicji jak wygląda złożenie R z R? Przyrównaj ten zbiór do R i zastanów się co z tego wynika. W drugą stronę to tak samo, definicja i przypatrzec się odpowiedniemu kwantyfikatorowi. Taka mała wskazówka. Zakładam że jest to relacja binarna. Takie relacje można reprezentować za pomocą grafów, a fakt bycia w relacji oznaczyć strzałkami. No i o złożeniu relacji samej ze sobą możemy myśleć tak. Jeśli (x,y) ∊ R ◦ R, to oznacza, że istnieje ścieżka długości 2 w tym narysowanym grafie. Albo mówiąc jeszcze inaczej, może dość z x do y w dwóch krokach. No to teraz zastanów się, jak reprezentuje się przechodniość na grafie. Wydaje mi się, że takie zobrazowanie powinno dać Ci lepsza intuicję. I znów gdyby ktoś się zastanawiał, rysunek jest poglądowy i nie spełnia założeń tego konkretnego zadania.