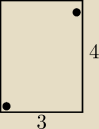
Zasada Dirichleta MmMmMm: Wewnątrz prostokąta o bokach długości 3 i 4 umieszczono 6 punktów. Udowodnij, że odległość między pewnymi dwoma punktami nie przekroczy √5 Nie rozumiem jak ta sytuacja ma być w ogóle możliwa, no bo przekątna tego prostokąta jest równa 5, a jak umieścimy dwa punkty w taki sposób jak np. na rysunku no to oczywiste jest że odległość między nimi wynosi więcej niż √5 więc jak mam udowodnić że jest inaczej ?

wredulus_pospolitus: masz podane, że pomiędzy dwoma PEWNYMI (czyli że jak umieścisz 6 punktów to nie znajdziesz żadnych dwóch których odległość jest większa od √5)

MmMmMm: Ach teraz już rozumiem, jak zwykle u mnie umiejętność czytania ze zrozumieniem jest na najwyższym poziomie. Domyślam się że trzeba podzielić jakoś ten prostokąt na 5 części i pokazać że nie można w tych częściach umieścić dwóch punktów tak, aby odległość między nimi była większa od √5, tylko w jaki sposób ?

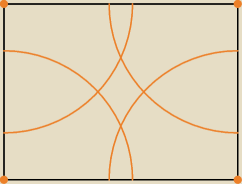
wredulus_pospolitus: proponuję −−− cztery ćwiartki okręgów o promieniu √5, piąty punkt na przecięciu się dwóch z tych ćwiartek (tak aby odległość tego punktu do dwóch innych była równa dokładnie √5) I patrzymy czy jest jakieś miejsce nie zajęte przez te okręgi/kawałki okręgów (aby móc umieścić tam szósty punkt)

wredulus_pospolitus: