rozne zadania z maty panda: pomoze ktos....? 1.w trapezie prostokatnym dluzsze ramie długosci 3√2 cm jest prostopadle do krótszej przekatnej oraz kat ostry trapezu ma miarę 30 stopni. *sporzadz rysunek(prosilabym bardzo) *Oblicz pole trapezu *Oblicz dlugosc dluzszej przekatnej trapezu 2.w trojkacie równoramiennym ABC w którym AC=BC,długośc dwusiecznej AD jest równa długosci odcinka CD.Oblicz miary katów w trojkacie ABCD. 3.Funkcja kwadratowa postaci f(x)=ax²+bx+c gdzie a≠0 przyjmuje artosc najwieksza fmax.=2 dla argumentu x=−1.Wiedzac ze wykres funkcji y=f(x) przechodzi przez punkt p=(√3−1,1/2): a) napisz wzor finkci w postaci kanoniocznej b)oblicz miejsca zerowe funkcji f i naszkicuj wykres y=f(x)

panda: POmoze ktos robilam zadani nr 2 i 3 ale nie zgadzaja mi sie wyniki takze nie wiem...licze na wasza pomoc

panda: to jak nikt nie pomoze....

Godzio: pomoge

Sabin: 3. postać kanoniczna: f(x) = a(x − p)² + q gdzie (p,q) − wspolrzedne wierzcholka paraboli u Ciebie p = −1, q = 2, czyli f(x) = a(x + 1)² + 2 wiadomo że punkt (√3−1, ¹₂) nalezy do wykresu, czyli za x podstawiamy pierwsza wspolrzedna, a za f(x) druga ¹₂ = a(√3 − 1 + 1)² + 2 ¹₂ − 2 = a√3² 3a = −³₂ a = −¹₂ czyli postac kanoniczna f(x) = −¹₂(x + 1)² + 2 miejsca zerowe: rozwin ta postac do postaci ogolnej i z delty...

Godzio:

	3√2
cos30o =
	b

	2
b = 3√2 *
	√3

	6√6
b =		= 2√6
	3

	d
tg30o =
	3√2

	√3
d =		* 3√2 = √6
	3

	a
sin30o =
	d

	1		√6
a =		* √6 =
	2		2

	h
cos30 =
	d

	√3		3√2
h =		* √6 =
	2		2

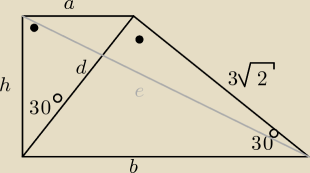
	a+b		2,5√6		3√2		15√3
P =		* h =		*		=
	2		2		2		4

h² + b² = e²

	3√2
(		)2 + 24 = e2
	2

e² = 28,5

	√114
e =
	2

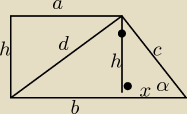
justka: c=3√2 , α=30

	h
sinα =
	c

√3		h
	=
2		3√2

h= ³₂√6

	x
cosαα=
	c

x = ³₂√2 b = a+x a² +h² = d² d² + c² = (a+x)² a² +h² + c²= (a+x)² h² +c² = 2ax + x² h² −x² +c²= 2ax

9		9
	*6 −		*2 + 18= 3√2a
4		4

	9
a =		√2
	2

b = a+ x b = 6√2

	1
P =		(a+b)h
	2

teraz podstaw i oblicz

panda: dziękuje a 2 ktos potrafi

panda: Mam pytanko czy to pole jest na pewno dobrze policzone...

panda: chodzi mi o pole z zad.1 od Godzia