pole czworokąta juliusz: Na rysunku kreskowane odcinki są równoległe do osi x. Jaka jest powierzchnia zacienionego czworoboku? https://zapodaj.net/images/581d7ccc7a925.png

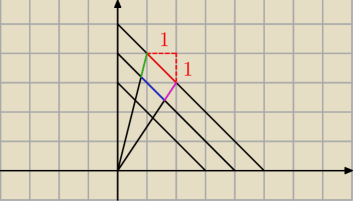
wredulus_pospolitus: 1) zauważamy, że czerwony bok jest przeciwprostokątną trójkąta o przyprostokątnych 1,1. Stąd jego długość to √2 2) zauważamy, że odcinek (0,0) − (1,4) jest dzielony przez kolejne równolegle do siebie odcinki ... związku z tym każdy z tych odcinków jest sobie równy

	1		√17
3) Stąd zielony =		√42 + 12 =
	5		5

	1		√13
4) Oraz fioletowy =		√32 + 22 =
	5		5

5) zauważamy, że trójkąty o wierzchołki (0,0) i podstawie czerwonej i niebieskiej są podobne, związku z tym że wiemy (2), to:

	4		4√2
niebieski =		czerwony =
	5		5

6) Masz boki czworokąta ... możesz wyznaczyć jego pole.

mix:

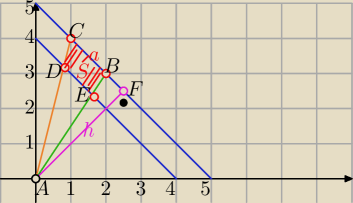
	5√2
|BC|=a=√2 |AF=h=
	2

	1
P(ABC)=P=		ah =5/2
	2

	9
ΔADE∼ΔABC w skali k=4/5 to S=		P
	25

	9		5
S=		*
	25		2

S=0,9