Dwumian Newtona Szkolniak:

	2
W rozwinięciu dwumianowym wyrażenia (x5−		)12 znaleźć współczynnik przy x20.
	x3

Prosiłbym o sprawdzenie poprawności rozwiązania, bo mam wątpliwości..

	2		12 k		−2
(x5−		)12=∑k=012		(x5)12−k(		)k=
	x3				x3

	12 k
=∑k=012		x60−5k(−2x−3)k=

	12 k
=∑k=012		x60−5k(−2)k*x−3k=

	12 k
=∑k=012		x60−8k(−2)k

Szukamy wartości 'k': 60−8k=20 ⇔ k=5

	12 5
Współczynnik równy jest:		(−2)5, czy jest dobrze?

Mila: Dobrze.

Szkolniak: Dziękuję Mila!

Mila: Dla Szkolniaka i maturzystów. W trójkącie ABC na boku BC leży punkt M, na boku AC leży punkt N, a odcinki AM i BN przecinają się w punkcie P. Mając dane stosunki BM: MC=m i AN: NC=n obliczyć stosunki AP: PM i BP: PN.

chichi: Ciekawi mnie, który maturzysta rozwiąże to zadanie. Zapewne żaden, choć chciałbym aby rozwiązali je wszyscy. Ja wstawię rozwiązanie jak nikt się nie zainteresuje

Mila: chichi Na razie nie wstawiaj, nawet wiem z czego skorzystasz.

chichi: @Mila tak poczekam do jutra wieczora, o ile nie wyprzedzi mnie @Eta pod innym nickiem

mat:

	(m+1)n
|AP| : |PM| =
	m

	(n+1)m
|BP| : |PN|=
	n

Mila: mat− zgadza się. Z czego skorzystałeś?

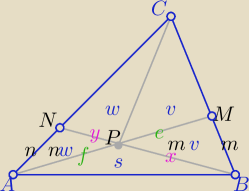
mat: mw,w,nv,v,s −− pola odpowiednich trójkątów [w+(m+1)v]n=nw+s ⇒ s=(m+1)vn

x		s		v
	=		= (m+1)*
y		nw		w

	v		(n+1)m
oraz [(n+1)w+v]m=mv+(m+1)vn ⇒		=
	w		(m+1)n

to ♣♣♣♣♣♣♣♣♣

x		(n+1)m
	=
y		n

♥♥♥♥♥♥♥♥♥♥ i

	f		s		(m+1)vn
		=		=
	e		vm		vm

	f		(m+1)n
		=
	e		m

♦♦♦♦♦♦♦♦♦♦♦♦

Mila: Dziękuje. Ja: I sposób− 2 razy tw. Menelausa. II sposób− Ceve i pola.

mat: