Kombinatoryka hops: Na okręgu a środku O i promieniu równym 1 zaznaczono punkty A, B, C, D, które są wierzchołkami kwadratu. Spośród wierzcholków tego kwadratu w sposób losowy wybrano dwa. Oblicz, ile w ten sposób można otrzymać odcinków łączących wybrane punkty, których długość jest równa √2

wredulus_pospolitus: Mamy kwadrat o boku 1. Na ile sposób można wybrać dwa wierzchołki w taki sposób, aby odcinek je łączący był przekątną tego kwadratu? Odpowiedź: Na 2 sposoby A−C lub B−D.

janek191: Boki tego kwadratu mają długość równą √2

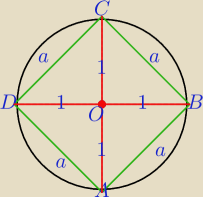
Mila: a=√2 Wypisz wszystkie możliwości, potem zastanów się jak obliczyć nie wypisując.