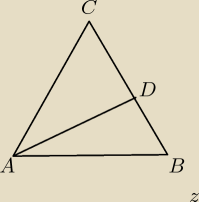
zadanie z informatora slawek: Zadanie 107. Punkt D leży na boku BC trójkąta równoramiennego ABC, w którym AC = BC . Odcinek AD dzieli trójkąt ABC na dwa trójkąty równoramienne w taki sposób, że AD = CD oraz AB = BD (patrz rysunek). Udowodnij, że |<ADC| = 5*|<ACD| .

Sabin: Oznaczmy |<DAC| = x, |<DAB| = y, |<ABD| = z Z warunkow zadania wynika, ze |<ACD| = x, |<ADB| = y Z wlasnosci stosowanych w tym zadaniu mamy, ze: (1) z = x + y (trojkat rownoramienny) (2) z + 2y = 180 (trojkat ABD) kat |<ADC| = y + z, wiec mamy dodatkowo z trojkata ADC (3) y + z + 2x = 180 z rownania (2) mamy: z + y + y = 180 z + y = 180 − y wstawmy to do (3) 180 − y + 2x = 180 y = 2x to wstawmy do (1) z = x + 2x = 3x stad |<ADC| = y + z = 5x, a za x przyjelismy |<DAC| ktory jest rowny mierze |<ACD|