Oblicz
KK: Ile rozwiązań całkowitych ma równanie 2x + 3y = 1?
31 paź 09:24
I'm back:
Nieskończenie wiele
31 paź 09:39
olek:
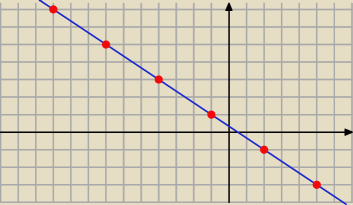
31 paź 11:59
Mila:
Równanie diofantyczne:
2x + 3y = 1
Szukamy rozwiązania:
| | 1−3y | | −2y−y +1 | |
2x=1−3y⇔x= |
| = |
| ⇔ |
| | 2 | | 2 | |
dla 1−y=2 mamy: y=−1 i x=2
(x
0,y
0)=(2,−1)
Równanie ma nieskończenie wiele rozwiązań w zbiorze liczb całkowitych.
x=x
0+3n
y=y
0−2n, gdzie n∊C
−−−−−−−−−
x=2+3n
y=−1−2n
==========
31 paź 16:13
